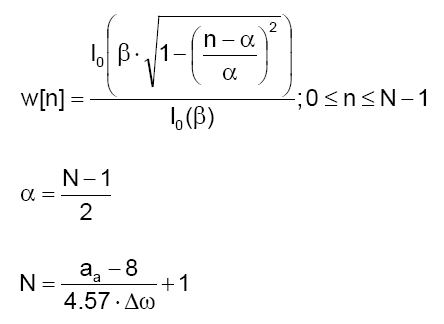2.3 Window functions
The window method is most commonly used method for designing FIR filters. The simplicity of design process makes this method very popular.
A window is a finite array consisting of coefficients selected to satisfy the desirable requirements. This chapter provides a few methods for estimating coefficients and basic characteristics of the window itself as well as the result filters designed using these coefficients. The point is to find these coefficients denoted by w[n].
When designing digital FIR filters using window functions it is necessary to specify:
-
- A window function to be used; and
-
- The filter order according to the required specifications (selectivity and stopband attenuation).
These two requirements are interrelated. Each function is a kind of compromise between the two following requirements:
-
- The higher the selectivity, i.e. the narrower the transition region; and
-
- The higher suppression of undesirable spectrum, i.e. the higher the stopband attenuation.
Table 2-3-1 below contains all window functions mentioned in this chapter and briefly compares their selectivity and stopband attenuation.
| WINDOW FUNCTION |
NORMALIZED LENGTH OF THE MAIN LOBE FOR N=20 |
TRANSITION REGION FOR N=20 |
MINIMUM STOPBAND ATTENUATION OF WINDOW FUNCTION |
MINIMUM STOPBAND ATTENUATION OF DESIGNED FILTER |
|---|
| Rectangular |
0.1π |
0.041π |
13 dB |
21 dB |
| Triangular (Bartlett) |
0.2π |
0.11π |
26 dB |
26 dB |
| Hann |
0.21π |
0.12π |
31 dB |
44 dB |
| Bartlett-Hanning |
0.21π |
0.13π |
36 dB |
39 dB |
| Hamming |
0.23π |
0.14π |
41 dB |
53 dB |
| Bohman |
0.31π |
0.2π |
46 dB |
51 dB |
| Blackman |
0.32π |
0.2π |
58 dB |
75 dB |
| Blackman-Harris |
0.43π |
0.32π |
91 dB |
109 dB |
Table 2-3-1. Comparison of window functions
Special attention should be paid to the fact that minimum attenuation of window function and that of the filter designed using that function are different in most cases. The difference, i.e. additional attenuation occurs under the process of designing a filter using window functions. This affects the stopband attenuation to become additionally higher, which is very desirable.
However, a drawback of this method is that the minimum stopband attenuation is fixed for each function. The exception is the Kaiser window described later in this chapter.
The following concepts such as the main lobe, main lobe width, side lobes, transition region, minimum stopband attenuation of window function and minimum stopband attenuation of designed filter are described in more detail in Figure 2-3-1.
Figure 2-3-1. Main lobe, main lobe width, side lobes, transition region
As can be seen in the table 2-3-1 above, the stopband attenuation of these windows is not adjustable. It is only possible to affect the transition region by increasing the filter order. For this reason it is preferable to start design process by specifying the appropriate window function on the basis of the stopband attenuation. It is most preferable to specify a window with the least stopband attenuation that satisfies the given requirements. This enables the designed filter to have the narrowest transition region.
Example:
Design a filter with the following characteristics:
-
- Minimum stopband attenuation is 40dB;
-
- Transition region between 2KHz and 3KHz; and
-
- Sampling frequency 10KHz.
Looking at the table 2-3-1 above (last column), it is obvious that required attenuation can be reached using the Hann window. Besides, such attenuation can be obtained using any other window following the Hann window (all the functions are sorted according to their stopband attenuation), thus the higher stopband attenuation would be at a cost of the wider transition region for the same filter order. Since the filter specification also includes transition region, this would further result in increasing the filter order and its complexity as well.
After specifying the suitable window function, it is necessary to compute the filter order. The cut-off frequencies of transition regions are normalized first.
-
- The sampling frequency is fs=10KHz;
-
- The lower cut-off frequency of transition region is f1=2KHz; and
-
- The upper cut-off frequency of transition region is f2=3KHz.
Normalized frequencies are obtained in the following way:
Transition region of the Hann window is 0.12π for a 20th order filter. To satisfy the given specifications, the required transition region is expressed as:
fn2 - fn1 = 0.2π
Since the required transition region is wider than that of a 20th order filter, the filter order needs to be less than 20. It is found via iteration. Roughly estimated, the initial solution in this case can be a 12th order filter. The required order is somewhat higher and is found after performing several iterations. The resulting filter order is 16.
Filter Designer Tool is used for obtaining a first-order filter. The table 2-3-2 provides performed iterations and other important information.
| NUMBER OF ITERATION |
FILTER ORDER |
FILTER ATTENUATION AT 3KHZ |
|---|
| 1 |
12 |
25 dB |
| 2 |
14 |
33 dB |
| 3 |
16 |
49 dB |
| 4 |
15 |
38 dB |
Table 2-3-2. Calculating filter order
After specifying the window function and filter order, it is necessary to compute window coefficients w[n] using expressions for the specified window.
2.3.1 Rectangular Window
The rectangular window is rarely used for its low stopband attenuation. The first lobe (refer to Figure 2-3-2) has attenuation of 13dB and the narrowest transition region, therefore. A filter designed using this window has minimum stopband attenuation of 21 dB.
Unlike other window functions being a kind of compromise between requirements for as narrow transition region as possible and as high stopband attenuation as possible, this window is characterized by extreme values. Namely, the minimum transition region is achieved, but at a cost of stopband attenuation.
It is easy to find rectangular window coefficients as all coefficients between 0 and N-1 (N-filter order) are equal to 1, which can be expressed in the following way:
w[n] = 1; 0 ≤ n ≤ N−1
Note that the rectangular window performs selection of N samples from a sequence of input samples, but it does not perform sample scaling.
Figure 2-3-2 illustrates coefficients in the time-domain.
Figure 2-3-2. Rectangular window in the time domain
Figure 2-3-3 illustrates the frequency domain of rectangular window
Figure 2-3-3. Rectangular window in the frequency domain (spectrum)
For its less stopband attenuation, the rectangular window is not preferable for digital filter design. Such a less attenuation is a result of cut-off samples within a window (a sequence of sampled frequencies). Up to a zero sample (from which sampling starts), all sampled frequencies are equal to zero. The first sample represents a sudden jump to some value (non-zero sample). Exactly these sudden jumps result in producing relatively sharp high-frequency components which lessen the stopband attenuation.
The attenuation gets higher by making cut-off samples less sharp, which results in reducing filter selectivity, i.e. wider transition region. Since initial requirements of a digital filter are predefined and due to less selectivity, it is necessary to increase the filter order to narrow the transition region. Note the fact that the transition region is inversely proportional to the filter order N. The transition region narrows as the filter order increases.
Increase in filter order affects the filter to become more complex and need more time for sample processing. This is why it is very important to be careful when specifying the window function and filter order as well.
2.3.2 Triangular (Bartlett) window
The triangular (Bartlett) window is one among many functions that lessens the effects of final samples. Due to it, the stopband attenuation of this window is higher than that of the rectangular window, whereas the selectivity is less. Namely, filters designed using this window have wider transition region than those designed using the rectangular window. As a result, it is necessary to have a higher order filter in order to keep the same tansition region as that of the filters designed with the rectangular window. This is the price to pay for producing the higher attenuation.
This function also represents a kind of compromise between requirements for as narrow transition region as possible and as higher stopband attenuation as possible, where the transition region is considered more important characteristic.
One of the advantages of designing filter using the triangular window is the simplicity of computing coefficients.
The triangular window coefficients can be expressed as:
Figure 2-3-4 illustrates coefficients in the time-domain.
Figure 2-3-4. Triangular window coefficients in the time-domain
Figure 2-3-5. illustrates the coefficients spectrum of the triangular window shown in Figure 2-3-4.
Figure 2-3-5. Triangular (Bartlett) window in the frequency domain (spectrum)
The attenuation of triangular window is low for most digital filter applications, but it is considerably higher than that for rectangular window. In some cases, when high attenuations are not needed, this filter can be used because it provides an easy way of computing coefficients.
2.3.3 Hann Window
The Hann window is used to lessen bad effects on frequency characteristic produced by the final samples of a signal being filtered. Digital filters designed with this window have higher stopband attenuation than those designed with triangle function. The first side lobe in the frequency domain of this filter has 31dB attenuation, whereas it amounts to 44dB in the designed filter. The transition region is the same as for triangular window, which makes this function one of the most desirable for designing.
Another advantage of this window is the ability to realtively fast increase the stopband attenuation of the following lobes. Already the second lobe has 41dB attenuation, whereas it amounts to 54dB for the designed filter. Refer to Figure 2-3-7 illustrating the coefficients of the Hann window.
The Hann window belongs to a class of generalized cosine windows which will be discussed in more details at the end of this chapter.
The Hann window coefficients can be expressed as:
Figure 2-3-6. illustrates the Hann window coefficients in the time domain.
Figure 2-3-6. The Hann window coefficients in the time domain
Figure 2-3-7. The Hann window coefficients in the frequency domain
As seen from the table 2-3-1, the transition region of Hann window is wider than that of triangular window. The difference is that the transition region of triangular window is computed in terms of -26dB attenuation, and in terms of -31dB attenuation for Hann window Accordingly, the conclusion is that Hann window has sharper fall than triangular one, which is considered as its advantage.
For the same requirements for minimum attenuation, the Hann window will have a narrower transition region.
2.3.4 Bartlett-Hanning Window
The Bartlett-Hannign window is another compromise between requirements for as narrow transition region as possible and as higher stopband attenuation as possible. The stopband attenuation of a filter designed with this window amounts to 39dB which is not at all a large value.
The Bartlett-Hanning window coefficients are expressed as:
This window is in fact a combination of triangular (Bartlett) and Hann window and has higher minimum stopband attenuation than both of them. Considering that the transition region is almost the same as for triangular and Hann window, this function is one of most commonly used windows.
Figure 2-3-8. illustrates the Bartlett-Hanning window coefficients in the time domain.
Figure 2-3-8. The Bartlett-Hanning window coefficients in the time domain
Figure 2-3-9. The Bartlett-Hanning window coefficients in the frequency domain
When the stopband attenuation doesn’t need to be higher than 39dB, the Bartlett-Hanning window is one of the best solutions to use. As seen in Figure 2-3-9, the side lobes increase attenuation, which is one of very desirable characteristics of digital filters.
2.3.5 Hamming Window
The Hamming window is one of the most popular and most commonly used windows. A filter designed with the Hamming window has minimum stopband attenuation of 53dB, which is sufficient for most implementations of digital filters. The transition region is somewhat wider than that of the Hann and Bartlett-Hanning windows, whereas the stopband attenuation is considerably higher. Unlike minimum stopband attenuation, the transition region can be changed by changing the filter order. The transition region narrows, whereas the minimum stopband attenuation remains unchanged as the filter order increases.
The Hamming window coefficients are expressed as:
The Hamming window belongs to a class of generalized cosine functions which are described in more details at the end of this chapter.
Figure 2-3-10 illustrates the Hamming window coefficients in the time domain.
Figure 2-3-10. The Hamming window coefficients in the time domain
Figure 2-3-11. The Hamming window coefficients in the frequency domain
Figure 2-3-11 illustrates the Hamming window in the frequency domain. As seen, the first side lobe is attenuated, so that the minimum stopband attenuation is defined in terms of the second side lobe and amounts to 41dB. All side lobes have almost the same maximum values (about -45dB).
2.3.6 Bohman Window
The Bohman window is a convolution of two semi-periods of a cosine function. The transition region and the main lobe are wider than those for Hamming window, but the stopband attenuation is higher, therefore. The attenuation of the first side lobe for Bohman window is 46dB, whereas the filters designed with Bohman window have the stopband attenuation of 51dB.
The Bohman window coefficients are expressed as:
Figure 2-3-12 illustrates the Bohman window coefficients in the time domain, whereas Figure 2-3-13 illustrates its coefficients in the frequency domain.
Figure 2-3-12. The Bohman window coefficients in the time domain
Figure 2-3-13. The Bohman window coefficients in the frequency domain
Figure 2-3-13 illustrates the Bohman window coefficients in the frequency domain. As seen, the first side lobe has minimum attenuation of 46dB, whereas for designed filter it amounts to 51dB. The attenuation increases relatively fast. The second side lobe in the Bohman window frequency domain has the attenuation of 61dB, whereas for the filters designed with this window it amounts to 65dB. It should be noted that side lobes of such filters are different than shown in Figure 2-3-13.
With regard to minimum attenuation as well as to mid-wide transition region, it can be concluded that Bohman window is suitable for most applications.
2.3.7 Blackman Window
The Blackman window is, along with Kaiser, Hamming and Blackman-Harris windows, considered most commonly used and the most popular windows. Relatively high attenuation makes this window very convenient for almost all applications. The minimum stopband attenuation of a filter designed with this window amounts to 75dB.
The Blackman window coefficients are expressed as:
Figure 2-3-14 illustrates the Blackman window coefficients in the time domain, whereas Figure 2-3-15. illustrates its coefficients in the frequency domain.
Figure 2-3-14. The Blackman window coefficients in the time domain
Figure 2-3-15. The Blackman window coefficients in the frequency domain
As seen from Figure 2-3-15, the Blackman window frequency domain reminds of the Hann window frequency domain. The difference is in attenuation of the first side lobe which amounts to 51dB, as well as in the main lobe which is somewhat wider. The side lobes, following the first one, cause additional stopband attenuation.
2.3.8 Blackman-Harris Window
The Blackman-Harris window is definately one of the most well-known and most commonly used windows. It is characterized by high stopband attenuation and the widest transition region comparing to all windows mentioned in this chapter. However, increase in filter order (more complex filter) cannot affect the minimum stopband attenuation, but affects the transition region.
The Blackman-Harris window has almost twice as wide transition region than, say, the Hamming window. Such a drawback (wide transition region) can be overcome by increasing the filter order. The result is a higher order filter (comparing to one designed with Hamming window) with twice as high stopband attenuation. It should be noted that the transition region of the Hamming window ranges between − 3dB and − 41dB (decrease of 38dB), whereas for Blackman-Harris window it is decreased by 88dB (from − 3dB to − 91dB ).
The Blackman-Harris window has minimum stopband attenuation of 91dB, whereas for the filters designed with this window it amounts to 109dB. Such an attenuation is sufficient for any digital filter application. If it is possible to support a filter order that will be required by this window, then the Blackman-Harris window is probably the best soultion.
The Blackman-Harris window coefficients are expressed as:
Figure 2-3-16. illustrates the Blackman-Harris window coefficients in the time domain, whereas Figure 2-3-16. illustrates its coefficients in the frequency domain.
Figure 2-3-16. The Blackman-Harris window coefficients in the time domain
Figure 2-3-17. The Blackman-Harris window coefficients in the frequency domain
Figure 2-3-17. illustrates the main characteristics of the Blackman-Harris window in the frequency domain. As seen, the main lobe is wide and the first side lobe is suppressed. Minimum stopband attenuation is determined by the second side lobe having the minimum attenuation of 91dB. The attenuation of other side lobes gradually increases.
2.3.9 Blackman-Harris Window
The generalized cosine functions are a type of window functions whose coefficients can be obtained via expression:
There are some window functions that also belong to this class. These are:
Each of these window functions is only a variation of the expression above. Their coefficients a, b and c are given in the table 2-3-3 below.
| WINDOW FUNCTION |
A |
B |
C |
|---|
| Rectangular |
1 |
0 |
0 |
| Hann |
0.5 |
0.5 |
0 |
| Hamming |
0.54 |
0.46 |
0 |
| Blackman |
0.42 |
0.5 |
0.08 |
Table 2-3-3. The coefficients of generalized cosine window functions
2.3.10 Kaiser Window
As you know, each of the windows described above is a kind of compromise between requirements for as narrow transition region as possible (greater selectivity) and as higher stopband attenuation as possible.
Comparing Hann and Bartlett-Hanning windows, it is obvious that both of them have the same transition region, but the Bartlett-Hanning window has higher attenuation. There is one more thing of concern which says that the minimum stopband attenuation depends on the specified window, whereas an increase in filter order affects the transition region.
All this leads us to the conclusion that the windows described here are not optimal. An optimal window is a function that has maximum attenuation according to the given width of the main lobe. The optimal window is also known as Kaiser window.
Its coefficients are expressed as:
where aa is the minimum stopband attenuation, and Δ ω is the width of (normalized) transition region. The order of band-pass and band-stop filters, obtained from the expression above, should be multiplied by 2.
The value of parameter β can be obtained from the table 2-3-4.
| AA |
Β |
|---|
| less than 21 |
0 |
| between 21 and 50 |
0.5842(aa - 21)^0.4 + 0.07886(aa - 21) |
| more than 50 |
0.1102(aa - 8.7) |
Table 2-3-4. Values of parameter β
I0(*) is a modified zero order Bessel function of the first kind. It can be approximated via expression:
In most practical cases it is sufficient to consider the first 20 elements of this order.
As can be seen from all mentioned above, in order to design an optimal Kaiser filter it is necessary to know normalized width of transition region as well as minimum desirable stopband attenuation.
Example:
What would a filter design with Kaiser window look like if we take into consideration the requirements given at the beginning of this chapter? The result of a filter designed with the Hann window is a 16th order filter.
Assuming that it is required to design a filter with the following characteristics:
-
- Minimum stopband attenuation is 40dB (aa);
-
- Transition region is between 2KHz and 3KHz (f1, f2); and
-
- Sampling frequency is 10KHz (fs).
Transition region:
The specified filter order is N=12. It means that the needed filter order is less by 4 than that obtained with the Hann window.
It is important to say that all the expressions above are obtained in an empirical way, which means that there will be some exceptions and variations in practice. For example, the expression used to compute the filter order gives accurate results in approximately 98% cases. Otherwise, the resulting filter order should be changed. Fortunately, the changes to be made are slight, and the filter order is increased or decreased by 2 at most.