2.4 Examples
This chapter discusses various FIR filter design methods. It also provides examples of all types of filters as well as of all methodes described in the previous chapters. The four standard types of filters are used here:
The design method used here is known as the window method.
The FIR filter design process can be split into several steps as described in Chapter 2.2.4 entitled
Designing FIR filters using window functions. These are:
-
- Defining filter specifications;
-
- Specifying a window function according to the filter specifications;
-
- Computing the filter order according to the filter specifications and specified window function;
-
- Computing the coefficients of the window;
-
- Computing the ideal filter coefficients according to the filter order;
-
- Computing the FIR filter coefficients according to the obtained window function and ideal filter coefficients; and
-
- If the resulting filter has too wide or too narrow transition region, it is necessary to change the filter order. The specified filter order is increased or decreased according to needs, and steps 4, 5 and 6 are repeated after that as many times as needed.
Depending on the window function in use, some steps will be skipped. If the filter order is known, step 3 is skipped. If the window function to use is predetermined, step 2 is skipped.
In every given example, the FIR filter design process will be described through these steps in order to make it easier for you to note similarities and differencies between various design methodes, window functions and design of various types of filters as well.
2.4.1 Filter design using Rectangular window
2.4.1.1 Example 1
Step 1:
Type of filter – low-pass filter
Filter specifications:
-
- Sampling frequency – fs=20KHz
-
- Passband cut-off frequency – fc=2.5KHz
Step 2:
Method – filter design using rectangular window
Step 3:
Filter order is predetermined, N=10;
A total number of filter coefficients is larger by one, i.e. N+1=11; and
Coefficients have indices between 0 and 10.
Step 4:
All coefficients of the rectangular window have the same value equal to 1.
w[n] = 1 ; 0 ≤ n ≤10
Step 5:
The ideal low-pass filter coefficients (ideal filter impulse response) are expressed as:
where M is the index of middle coefficient.
Normalized cut-off frequency ωc can be calculated using the following expression:
The values of coefficients (rounded to six digits) are obtained by combining the values of M and ωc with expression for the impulse response coefficients of the ideal low-pass filter:
The middle element is found via the following expression
 Step 6:
Step 6:
The designed FIR filter coefficients are obtained via the following expression:
The FIR filter coefficients h[n] rounded to 6 digits are:
Step 7:
The filter order is predetermined.
There is no need to additionally change it.
Filter realization:
Figure 2-4-1 illustrates the direct realization of designed FIR filter, whereas Figure 2-4-2 illustrates the optimized realization of designed FIR filter, which is based on the fact that all FIR filter coefficients are, for the sake of linear phase characteristic, symmetric about their middle element.
Figure 2-4-1. FIR filter direct realization
Figure 2-4-2. Optimized realization structure of FIR filter
2.4.1.2 Example 2
Step 1:
Type of filter – high-pass filter
Filter specifications:
-
- Sampling frequency– fs=20KHz
-
- Passband cut-off frequency – fc=5KHz
Step 2:
Method – filter design using rectangular window
Step 3:
Filter order is predetermined, N=8;
A total number of filter coefficients is larger by 1, i.e. N+1=9;
Coefficients have indices between 0 and 8.
Step 4:
All coefficients of the rectangular window have the same value equal to 1.
w[n] = 1 ; 0 ≤ n ≤ 8
Step 5:
The ideal high-pass filter coefficients (ideal filter impulse response) are expressed as:
where M is the index of middle coefficient.
Normalized cut-off frequency ωc can be calculated using the following expression:
The values of coefficients (rounded to six digits) are obtained by combining the values of M and ωc with expression for the impulse response coefficients of the ideal low-pass filter:
Step 6:
The designed FIR filter coefficients are found via expression:
The FIR filter coefficients h[n] rounded to 6 digits are:
Step 7:
The filter order is predetermined.
There is no need to additionally change it.
Filter realization:
Figure 2-4-3 illustrates the direct realization of designed FIR filter, whereas figure 2-4-4 illustrates the optimized realization of designed FIR filter which is based on the fact that all FIR filter coefficients are, for the sake of linear phase characteristic, symmetric about their middle element.
Figure 2-4-3. FIR filter direct realization
Figure 2-4-4. FIR filter optimized realization structure
2.4.1.3 Example 3
Step 1:
Type of filter – band-pass filter
Filter specifications:
-
- Sampling frequency – fs=20KHz
-
- Passband cut-off frequency – fc1=3KHz, fc2=5.5KHz
Step 2:
Method – filter design using rectangular window
Step 3:
Filter order is predetermined, N=14
A total number of filter coefficients is larger by 1, i.e. N+1=15.
Coefficients have indices between 0 and 14.
Step 4:
All coefficients of the rectangular window have the same value equal to 1.
w[n] = 1 ; 0 ≤ n ≤14
Step 5:
The ideal high-pass filter coefficients (ideal filter impulse response) are expressed as:
where M is the index of middle coefficient.
Normalized cut-off frequencies ωc1 and ωc2 can be found using the following expressions:
The values of coefficients (rounded to six digits) are obtained by combining the values of M and ωc1 and ωc2 with expression for the impulse response coefficients of the ideal band-pass filter:
Step 7:
Filter order is predetermined.
There is no need to additionally change it.
Filter realization:
Figure 2-4-5 illustrates the direct realization of designed FIR filter, whereas figure 2-4-6 illustrates optimized realization of designed FIR filter which is based on the fact that all FIR filter coefficients are, for the sake of linear phase characteristic, symmetric about their middle element.
Figure 2-4-5. FIR filter direct realization
Figure 2-4-6. FIR filter optimized realization structure
2.4.1.4 Example 4
Step 1:
Type of filter – band-stop filter
Filter specifications:
-
- Sampling frequency – fs=20KHz
-
- Stopband cut-off frequency - fc1=3KHz, fc2=5.5KHz
Step 2:Method – filter design using rectangular windowStep 3:
Filter order is predetermined, N=14;
A total number of filter coefficients is larger by 1, i.e. N+1=15; and
Coefficients have indices between 0 and 14.
Step 4:
All coefficients of the rectangular window have the same value equal to 1.
w[n] = 1 ; 0 ≤ n ≤ 14
Step 5:
The ideal high-pass filter coefficients (ideal filter impulse response) are expressed as:
where M is the index of middle coefficient.
Normalized cut-off frequencies ωc1 and ωc2 can be found using expressions:
The values of coefficients (rounded to six digits) are obtained by combining the values of M and ωc1 and ωc2 with expression for the impulse response coefficients of the ideal band-stop filter:
Note that, excepting the middle element, all coefficients are the same as in the previous example (band-pass filter with the same cut-off frequencies), but have the opposite sign.
Step 6:
The designed FIR filter coefficients are found via expression:
The FIR filter coefficients h[n], rounded to 6 digits, are:
Step 7:
Filter order is predetermined.
There is no need to additionally change it.
Filter realization:
Figure 2-4-7 illustrates the direct realization of designed FIR filter, whereas figure 2-4-8 illustrates optimized realization of designed FIR filter which is based on the fact that all FIR filter coefficients are, for the sake of linear phase characteristic, symmetric about their middle element.
Figure 2-4-7. FIR filter direct realization
Figure 2-4-8. FIR filter optimized realization structure
2.4.2 Filter design using Bartlett window
2.4.2.1 Example 1
Step 1:
Type of filter – low-pass filter
Filter specifications:
-
- Sampling frequency – fs=20KHz
-
- Passband cut-off frequency – fc=2.5KHz
Step 2:
Method – filter design using Barlett window
Step 3:
Filter order is predetermined, Nf=9;
A total number of filter coefficients is larger by 1, i.e. N=Nf+1=10; and
Coefficients have indices between 0 and 8.
Step 4:
The coefficients of Bartlett window are expressed as:
Step 5:
The ideal low-pass filter coefficients (ideal filter impulse response) are given in the expression below:
where M is the index of middle coefficient.
Since the value of M is not an integer, the middle element representing a center of coefficients symmetry doesn’t exist.
Normalized cut-off frequency ωc can be calculated using expression:
The values of coefficients (rounded to six digits) are obtained by combining the values of M and ωc with expression for the impulse response coefficients of the ideal low-pass filter:
Step 6:
The designed FIR filter coefficients are found via expression:
h[n] = w[n] * hd[n] ; 0 ≤ n ≤9
The FIR filter coefficients h[n] rounded to 6 digits are:
Step 7:
The filter order is predetermined.
There is no need to additionally change it.
Filter realization:
Figure 2-4-9 illustrates the direct realization of designed FIR filter, whereas figure 2-4-10 illustrates optimized realization of designed FIR filter which is based on the fact that all FIR filter coefficients are, for the sake of linear phase characteristic, symmetric about their middle element.
Figure 2-4-9. FIR filter direct realization
Figure 2-4-10. FIR filter optimized realization structure
2.4.2.2 Example 2
Step 1:
Type of filter – high-pass filter
Filter specifications:
-
- Sampling frequency – fs=20KHz
-
- Passband cut-off frequency – fc=5KHz
Step 2:
Method –filter design using Bartlett window
Step 3:
Filter order is predetermined, Nf=8;
A total number of filter coefficients is larger by 1, i.e. N=Nf+1=9;
Coefficients have indices between 0 and 8.
Step 4:
The Bartlett window function coefficients are found via expression:
Step 5:
The ideal high-pass filter coefficients (ideal filter impulse response) are expressed as:
where M is the index of middle coefficient.
Normalized cut-off frequency ωc may be calculated via the following expression:
The values of coefficients (rounded to six digits) are obtained by combining the values of M and ωc with expression for the impulse response coefficients of the ideal high-pass filter:
Step 6:
The designed FIR filter coefficients are found via expression:
h[n] = w[n] * hd[n] ; 0 ≤ n ≤ 8
The FIR filter coefficients h[n] rounded to 6 digits are:
Step 7:
Filter order is predetermined.
There is no need to additionally change it.
Filter realization:
Figure 2-4-11 illustrates the direct realization of designed FIR filter, whereas figure 2-4-12 illustrates optimized realization of designed FIR filter which is based on the fact that all FIR filter coefficients are, for the sake of linear phase characteristic, symmetric about their middle element.
Figure 2-4-11. FIR filter direct realization
Figure 2-4-12. FIR filter optimized realization structure
2.4.2.3 Example 3
Step 1:
Type of filter – band-pass filter
Filter specifications:
-
- Sampling frequency – fs=20KHz; and
-
- Passband cut-off frequencies – fc1=3KHz, fc2=5.5KHz.
Step 2:
Method – filter design using Bartlett window
Step 3:
Filter order is predetermined, Nf=14;
A total number of filter coefficients is larger by 1, i.e. N=Nf+1=15; and
Coefficients have indices between 0 and 14.
Step 4:
The Balett window coefficients are found via expression:
Step 5:
The ideal high-pass filter coefficients (ideal filter impulse response) are expressed as:
where M is the index of middle coefficient.
Normalized cut-off frequencies ωc1 and ωc2 can be calculated using expressions:
The values of coefficients (rounded to six digits) are obtained by combining the values of M and ωc1 and ωc2 with expression for the impulse response coefficients of the ideal band-pass filter:
Step 6:
The designed FIR filter coefficients are found via expression:
h[n] = w[n] * hd[n] ; 0 ≤ n ≤ 14
The FIR filter coefficients h[n] rounded to 6 digits are:
Step 7:
The filter order is predetermined.
There is no need to additionally change it.
Filter realization:
Figure 2-4-13 illustrates the direct realization of designed FIR filter, whereas figure 2-4-14 illustrates optimized realization structure of designed FIR filter which is based on the fact that all FIR filter coefficients are, for the sake of linear phase characteristic, symmetric about their middle element.
Figure 2-4-13. FIR filter direct realization
Figure 2-4-14. FIR filter optimized realization structure
2.4.2.4 Example 4
Step 1:
Type of filter – band-stop filter
Filter specifications:
-
- Sampling frequency – fs=20KHz; and
-
- Stopband cut-off frequencies – fc1=3KHz, fc2=5.5KHz.
Step 2:
Method – filter design using Bartlett window
Step 3:
Filter order is predetermined, Nf=14;
A total number of filter coefficients is larger by 1, i.e. N=Nf+1=15; and
Coefficients have indices between 0 and 14.
Step 4:
The coefficients of Bartlett window are found via expression:
Step 5:
The ideal high-pass filter coefficients (ideal filter impulse response) are expressed as:
where M is the index of middle coefficient.
Normalized cut-off frequencies ωc1 and ωc2 can be calculated using expressions:
The values of coefficients (rounded to six digits) are obtained by combining the values of M, ωc1 and ωc2 with expression for the impulse response coefficients of the ideal band-stop filter:
Note that, excepting the middle element, all the coefficients are the same as in the previous example (band-pass filter with the same cut-off frequencies), but have the opposite sign.
Step 6:
The designed FIR filter coefficients are found via expression:
h[n] = w[n] * hd[n] ; 0 ≤ n ≤ 14
The FIR filter coefficients h[n] rounded to 6 digits are:
Step 7:
The filter order is predetermined.
There is no need to additionally change it.
Filter realization:
Figure 2-4-15 illustrates the direct realization of designed FIR filter, whereas figure 2-4-16 illustrates optimized realization of designed FIR filter which is based on the fact that all FIR filter coefficients are, for the sake of linear phase characteristic, symmetric about their middle element.
Figure 2-4-15. FIR filter direct realization
Figure 2-4-16. FIR filter optimized realization structure
It is determined on purpose that FIR filters, explained in examples 3 and 4, have the same order. The similarity between the coefficients of band-pass and band-stop FIR filters is obvious. All coefficients of the band-stop FIR filter have the same absolute values as the corresponding coefficients of the band-pass FIR filter. The only difference is that they are of the opposite sign. The middle element of the band-stop filter is defined as:
bbs = 1 - bbp
where:
-
- bbs is the middle coefficient of the band-stop filter; and
-
- bbp is the middle coefficient of the band-pass filter.
Because of such similarity, it is easy to convert a band-pass FIR filter into a band-stop FIR filter having the same cut-off frequencies, sampling frequency and filter order.
Besides, low-pass and high-pass FIR filters are interrelated in the same way, which can be seen in examples describing Hann window.
2.4.3 Filter design using Hann window
2.4.3.1 Example 1
Step 1:
Type of filter – low-pass filter
Filter specifications:
-
- Sampling frequency – fs=20KHz; and
-
- Passband cut-off frequency – fc=2.5KHz.
Step 2:
Method – filter design using Hann window
Step 3:
Filter order is predetermined, Nf=10;
A total number of filter coefficients is larger by 1, i.e. N=Nf+1=11; and
Coefficients have indices between 0 and 10.
Step 4:
The Hann window function coefficients are found via expression:
Step 5:
The ideal low-pass filter coefficients (ideal filter impulse response) are expressed as:
where M is the index of middle coefficient.
Normalized cut-off frequency ωc can be calculated using expression:
The values of coefficients (rounded to six digits) are obtained by combining the values of M and ωc with expression for the impulse reaponse coefficients of the ideal low-pass filter:
Step 6:
The designed FIR filter coefficients are found via expression:
h[n] = w[n] * hd[n] ; 0 ≤ n ≤ 10
The FIR filter coefficients h[n] rounded to 6 digits are:
Step 7:
The filter order is predetermined.
There is no need to additionally change it.
Filter realization:
Figure 2-4-17 illustrates the direct realization of designed FIR filter, whereas figure 2-4-18 illustrates optimized realization structure of designed FIR filter which is based on the fact that all FIR filter coefficients are, for the sake of linear phase characteristic, symmetric about their middle element.
Figure 2-4-17. FIR filter direct realization
Figure 2-4-18. FIR filter optimized realization structure
2.4.3.2 Example 2
Step 1:
Filter type – high-pass filter Filter specifications:
-
- Sampling frequency – fs=20KHz; and
-
- Passband cut-off frequency – fc=2.5KHz.
Step 2:
Method –filter design using Hann window
Step 3:
Filter order is predetermined, Nf=10;
A total number of filter coefficients is larger by 1, i.e. N=Nf+1=11; and
Coefficients have indices between 0 and 10.
Step 4:
The Hann window function coefficients are found via expression:
Step 5:
The ideal high-pass filter coefficients (ideal filter impulse response) are expressed as:
where M is the index of middle coefficient.
Normalized cut-off frequency ωc can be calculated using expression:
The values of coefficients (rounded to six digits) are obtained by combining the values of M and ωc with expression for the impulse response coefficients of the ideal high-pass filter:
Step 6:
The designed FIR filter coefficients are found via expression:
h[n] = w[n] * hd[n] ; 0 ≤ n ≤ 10
The FIR filter coefficients h[n] rounded to 6 digits are:
Step 7:
The filter order is predetermined.
There is no need to additionally change it.
Filter realization:
Figure 2-4-19 illustrates the direct realization of designed FIR filter, whereas figure 2-4-20 illustrates optimized realization structure of designed FIR filter which is based on the fact that all FIR filter coefficients are, for the sake of linear phase characteristic, symmetric about their middle element.
Figure 2-4-19. FIR filter direct realization
Figure 2-4-20. FIR filter optimized realization structure
2.4.3.3 Example 3
Step 1:
Type of filter – band-pass filter
Filter specifications:
-
- Sampling frequency – fs=20KHz; and
-
- Passband cut-off frequency – fc1=3KHz, fc2=5.5KHz.
Step 2:
Method – filter design using Hann window
Step 3:
Filter order is predtermined, Nf=14;
A total number of filter coefficients is larger by 1, i.e. N=Nf+1=15; and
Coefficients have indices between 0 and 14.
Step 4:
The Hann window function coefficients are found via expression:
Step 5:
The ideal high-pass filter coefficients (ideal filter impulse response) are expressed as:
where M is the index of middle coefficient.
Normalized cut-off frequencies ωc1 and ωc2 can be calculated using expressions:
The values of coefficients (rounded to six digits) are obtained by combining the values of M, ωc1 and ωc2 with expression for the impulse response coefficients of the ideal band-pass filter:
Step 6:
The designed FIR filter coefficients are found via expression:
h[n] = w[n] * hd[n] ; 0 ≤ n ≤ 14
The FIR filter coefficients h[n] rounded to 6 digits are:
Step 7:
The filter order is predetermined.
There is no need to additionally change it.
Filter realization:
Figure 2-4-21 illustrates the direct realization of designed FIR filter, whereas figure 2-4-22 illustrates optimized realization structure of designed FIR filter which is based on the fact that all FIR filter coefficients are, for the sake of linear phase characteristic, symmetric about their middle element.
Figure 2-4-21. FIR filter direct realization
Figure 2-4-22. FIR filter optimized realization structure
2.4.3.3 Example 3
Step 1:
Type of filter – band-stop filter
Filter specifications:
-
- Sampling frequency – fs=20KHz; and
-
- Passband cut-off frequency – fc1=3KHz, fc2=5.5KHz.
Step 2:
Method – filter design using Hann window
Step 3:
Filter order is predetermined, Nf=14;
A total number of filter coefficients is larger by 1, i.e. N=Nf+1=15;
Coefficients have indices between 0 and 14.
Step 4:
The Hann window function coefficients are found via expression:
Step 5:
The ideal high-pass filter coefficients (ideal filter impulse response) are expressed as:
where M is the index of middle coefficient.
Normalized cut-off frequencies ωc1 and ωc2 can be calculated using expressions:
The values of coefficients (rounded to six digits) are obtained by combining the values of M, ωc1 and ωc2 with expression for the impulse response coefficients of the ideal band-stop filter:
Note that, excepting the middle element, all coefficients are the same as in the previous example (band-pass filter with the same cut-off frequencies), but have the opposite sign.
Step 6:
The designed FIR filter coefficients are found via expression:
h[n]=w[n] * hd[n] ; 0 ≤ n ≤ 14
The FIR filter coefficients h[n] rounded to 6 digits are:
Step 7:
The filter order is predetermined.
There is no need to additionally change it.
Filter realization:
Figure 2-4-23 illustrates the direct realization of designed FIR filter, whereas figure 2-4-24 illustrates optimized realization structure of designed FIR filter which is based on the fact that all FIR filter coefficients are, for the sake of linear phase characteristic, symmetric about their middle element.
Figure 2-4-23. FIR filter direct realization
Figure 2-4-24. FIR filter optimized realization structure
It is specified on purpose that FIR filters, explained in examples 1 and 2, have the same order. The similarity between low-pass and high-pass FIR filter coefficients is obvious. All coefficients of the low-pass FIR filter have the same absolute values as the corresponding coefficients of the high-pass FIR filter. The only difference is that they are of the opposite sign. The middle element is defined as:
blp = 1 - bhp
where:
-
- blp is the middle coefficient of a low-pass filter; and
-
- bhp is the middle coefficient of a high-pass filter.
Because of such similarity, it is easy to convert a low-pass FIR filter into a high-pass FIR filter having the same cut-off frequencies, sampiling frequency and filter order.
2.4.4 Filter design using Bartlett-Hanning window
2.4.4.1 Example 1
Step 1:
Type of filter – low-pass filter
Filter specifications:
-
- Sampling frequency – fs=22050Hz; and
-
- Passband cut-off frequency – fc=4KHz.
Step 2:
Method – filter design using Bartlett-Hanning window
Step 3:
Filter order is predetermined, Nf=9;
A total number of filter coefficients is larger by 1, i.e. N=Nf+1=10; and
Coefficients have indices between 0 and 9.
Step 4:
The Bartlett-Hanning window function coefficients are found via expression:
Step 5:
The ideal low-pass filter coefficients (ideal filter impulse response) are expressed as:
where M is the index of middle coefficient.
Normalized cut-off frequency ωc can be calculated using expression:
The values of coefficients (rounded to six digits) are obtained by combining the values of M and ωc with expression for the impulse response coefficients of the ideal low-pass filter:
Step 6:
The designed FIR filter coefficients are found via expression:
h[n] = w[n] * hd[n] ; 0 ≤ n ≤ 9
The FIR filter coefficients h[n] rounded to 6 digits are:
Step 7:
The filter order is predetermined.
There is no need to additionally change it.
Filter realization:
Figure 2-4-25 illustrates the direct realization of designed FIR filter, whereas figure 2-4-26 illustrates optimized realization structure of designed FIR filter which is based on the fact that all FIR filter coefficients are, for the sake of linear phase characteristic, symmetric about their middle element.
Figure 2-4-25. FIR filter direct realization
Figure 2-4-26. FIR filter optimized realization structure
2.4.4.2 Example 2
Step 1:
Type of filter – high-pass filter
Filter specifications:
-
- Sampling frequency – fs=22050Hz; and
-
- Passband cut-off frequency – fc=4KHz.
Step 2:
Method – filter design using Bartlett-Hanning window
Step 3:
Filter order is predetermined, Nf=10;
A total number of filter coefficients is larger by 1, i.e. N=Nf+1=11; and
Coefficients have indices between 0 and 10.
Step 4:
The Bartlett-Hanning window function coefficients are found via expression:
Step 5:
The ideal high-pass filter coefficients (ideal filter impulse response) are expressed as:
where M is the index of middle coefficient.
Normalized cut-off frequency ωc may be calculated using expression:
The values of coefficients (rounded to six digits) are obtained by combining the values of M and ωc with expression for the impulse response coefficients of the ideal high-pass filter:
Step 6:
The designed FIR filter coefficients are found via expression:
h[n] = w[n] * hd[n] ; 0 ≤ n ≤ 10
The FIR filter coefficients h[n] rounded to 6 digits are:
Step 7:
The filter order is predetermined.
There is no need to additionally change it.
Filter realization:
Figure 2-4-27 illustrates the direct realization of designed FIR filter, whereas figure 2-4-28 illustrates optimized realization structure of designed FIR filter which is based on the fact that all FIR filter coefficients are, for the sake of linear phase characteristic, symmetric about their middle element.
Figure 2-4-27. FIR filter direct realization
Figure 2-4-28. FIR filter optimized realization structure
2.4.4.3 Example 3
Step 1:
Type of filter – band-pass filter
Filter specifications:
-
- Sampling frequency – fs=22050Hz; and
-
- Passband cut-off frequency – fc1=2KHz, fc2=5KHz.
Step 2:
Method – filter design using Bartlett-Hanning window
Step 3:
Filter order is predetermined, Nf=12;
A total number of filter coefficients is larger by 1, i.e. N=Nf+1=13; and
Coefficients have indices between 0 and 12.
Step 4:
The Bartlett-Hanning window function coefficients are found via expression:
Step 5:
The ideal high-pass filter coefficients (ideal filter impulse response) are expressed as:
where M is the index of middle coefficient.
Normalized cut-off frequencies ωc1 and ωc2 can be calculated using expressions:
The values of coefficients (rounded to six digits) are obtained by combining the values of M, ωc1 and ωc2 with expression for the impulse response coefficients of the ideal band-pass filter:
Step 6:
The designed FIR filter coefficients are found via expression:
h[n] = w[n] * hd[n] ; 0 ≤ n ≤ 12
The FIR filter coefficients h[n] rounded to 6 digits are:
Step 7:
The filter order is predetermined.
There is no need to additionally change it.
Filter realization:
Figure 2-4-29 illustrates the direct realization of designed FIR filter, whereas figure 2-4-30 illustrates optimized realization structure of designed FIR filter which is based on the fact that all FIR filter coefficients are, for the sake of linear phase characteristic, symmetric about their middle element.
Figure 2-4-29. FIR filter direct realization
Figure 2-4-30. FIR filter optimized realization structure
2.4.4.4 Example 4
Step 1:
Type of filter – band-stop filter
Filter specifications:
-
- Sampling frequency – fs=22050Hz; and
-
- Passband cut-off frequencies – fc1=2KHz, fc2=6KHz.
Step 2:
Method – filter design using Bartlett-Hanning window
Step 3:
Filter order is predetermined, Nf=12;
A total number of filter coefficients is larger by 1, i.e. N=Nf+1=13; and
Coefficients have indices between 0 and 12.
Step 4:
The Bartlett-Hanning window function coefficients are found via expression:
Step 5:
The ideal high-pass filter coefficients (ideal filter impulse response) are expressed as:
where M is the index of middle coefficient.
Normalized cut-off frequencies ωc1 and ωc2 can be calculated using expressions:
The values of coefficients (rounded to six digits) are obtained by combining the values of M, ωc1 and ωc2 with expression for the impulse reaponse coefficients of the ideal band-stop filter:
Step 6:
The designed FIR filter coefficients are found via expression:
h[n] = w[n] * hd[n] ; 0 ≤ n ≤ 12
The FIR filter coefficients h[n] rounded to 6 digits are:
Step 7:
The filter order is predetermined.
There is no need to additionally change it.
Filter realization:
Figure 2-4-31 illustrates the direct realization of designed FIR filter, whereas figure 2-4-32 illustrates optimized realization structure of designed FIR filter which is based on the fact that all FIR filter coefficients are, for the sake of linear phase characteristic, symmetric about their middle element.
Figure 2-4-31. FIR filter direct realization
Figure 2-4-32. FIR filter optimized realization structure
2.4.5 Filter design using Hamming window
2.4.5.1 Example 1
Step 1:
Type of filter – low-pass filter
Filte specifications:
-
- Sampling frequency – fs=22050Hz;
-
- Passband cut-off frequency – fc1=3KHz;
-
- Stopband cut-off frequency – fc2=6KHz; and
-
- Minimum stopband attenuation – 40dB.
Step 2:
Method – filter design using Hamming window
Step 3:
For the first iteration, the filter order can be determined from the table 2-4-1 below.
| WINDOW FUNCTION |
NORMALIZED LENGTH OF THE MAIN LOBE FOR N=20 |
TRANSITION REGION FOR N=20 |
MINIMUM STOPBAND ATTENUATION OF WINDOW FUNCTION |
MINIMUM STOPBAND ATTENUATION OF DESIGNED FILTER |
|---|
| Rectangular |
0.1π |
0.041π |
13 dB |
21 dB |
| Triangular (Bartlett) |
0.2π |
0.11π |
26 dB |
26 dB |
| Hann |
0.21π |
0.12π |
31 dB |
44 dB |
| Bartlett-Hanning |
0.21π |
0.13π |
36 dB |
39 dB |
| Hamming |
0.23π |
0.14π |
41 dB |
53 dB |
| Bohman |
0.31π |
0.2π |
46 dB |
51 dB |
| Blackman |
0.32π |
0.2π |
58 dB |
75 dB |
| Blackman-Harris |
0.43π |
0.32π |
91 dB |
109 dB |
Table 2-4-1. Comparison of window functions
Using the specifications for the transition region of the required filter, it is possible to compute cut-off frequencies:
The required transition region of the filter is:
The transition region of the filter to be designed is approximately twice that of the filter given in the table above. For the first iteration, the filter order can be half of that.
-
- A total number of filter coefficients is larger by 1, i.e. N=Nf+1=11; and
-
- Coefficients have indices between 0 and 10.
Step 4:
The Hamming window function coefficients are found via expression:
Step 5:
The ideal low-pass filter coefficients (ideal filter impulse response) are expressed as:
where M is the index of middle coefficient.
Normalized cut-off frequency ωc can be calculated using expression:
The values of coefficients (rounded to six digits) are obtained by combining the values of M and ωc with expression for the impulse response coefficients of the ideal low-pass filter:
Step 6:
The designed FIR filter coefficients are found via expression:
h[n] = w[n] * hd[n] ; 0 ≤ n ≤ 10
The FIR filter coefficients h[n] rounded to 6 digits are:
Step 7:
Analyse in the frequency domain is performed using the Filter Designer Tool program.
Figure 2-4-33. Frequency characteristic of the resulting filter
Figure 2-4-33 illustrates the frequency characteristic of the resulting filter. It is obtained in the
Filter Designer Tool program. As seen, the resulting filter doesn’t satisfy the required specifications. The attenuation at the frequency of 6KHz amounts to 32.96dB only, which is not sufficient. It is necessary to increase the filter order.
Another way is to compute the attenuation at the frequency of 6KHz. Starting from the impulse response, the first thing that should be done is the Z-transform. It is explained, along with Fourier transformation, in chapter 2-2-2.
It is easy to obtain the Fourier transformation via the Z-transform:
According to the analyse performed using Filter Designer Tool, it is confirmed that the filter order has to be incremented.
The filter order is incremented by two. The whole process of designing filter is repeated from the step 3.
Step 3:
Filter order is Nf=12;
A total number of filter coefficients is larger by 1, i.e. N=Nf+1=13; and
Coefficients have indices between 0 and 12.
Step 4:
The Hamming window function coefficients are found via expression:
Step 5:
The ideal low-pass filter coefficients (ideal filter impulse response) are expressed as:
where M is the index of middle coefficient.
Normalized cut-off frequency ωc can be calculated using expression:
The values of coefficients (rounded to six digits) are obtained by combining the values of M and ωc with expression for the impulse response coefficients of the ideal low-pass filter:
Step 6:
The designed FIR filter coefficients are found via expression:
h[n] = w[n] * hd[n] ; 0 ≤ n ≤ 12
The FIR filter coefficients h[n] rounded to 6 digits are:
Step 7:
Analyse in the frequency domain is performed using the Filter Designer Tool program.
Figure 2-4-34. Frequency characteristic of the resulting filter
Figure 2-4-34 illustrates the frequency characteristic of the resulting filter. As seen, the resulting filter doesn’t satisfy the given specifications. The attenuation at the frequency of 6KHz amounts to 45.26dB only, which is not sufficient. It is necessary to change the filter order.
Filter realization:
Figure 2-4-35 illustrates the direct realization of designed FIR filter, whereas figure 2-4-36 illustrates optimized realization structure of designed FIR filter which is based on the fact that all FIR filter coefficients are, for the sake of linear phase characteristic, symmetric about their middle element.
Figure 2-4-35. FIR filter direct realization
Figure 2-4-36. FIR filter optimized realization structure
2.4.5.2 Example 2
Step 1:
Type of filter – high-pass filter
Filte specifications:
-
- Sampling frequency – fs=22050Hz; and
-
- Passband cut-off frequency – fc=4KHz.
Step 2:
Method – filter design using Hamming window
Step 3:
Filter order is predetermined, Nf=10;
A total number of filter coefficients is larger by 1, i.e. N=Nf+1=11; and
Coefficients have indices between 0 and 10.
Step 4:
The Hamming window function coefficients are found via expression:
The Hamming window function is one of rare standard windows where w[0] > 0 is in effect.
Step 5:
The ideal high-pass filter coefficients (ideal filter impulse response) are expressed as:
where M is the index of middle coefficient.
Normalized cut-off frequency ωc can be calculated using expression:
The values of coefficients (rounded to six digits) are obtained by combining the values of M and ωc with expression for the impulse response coefficients of the ideal high-pass filter:
Step 6:
The designed FIR filter coefficients are found via expression:
h[n] = w[n] * hd[n] ; 0 ≤ n ≤ 10
The FIR filter coefficients h[n] rounded to 6 digits are:
Step 7:
The filter order is predetermined.
There is no need to additionally change it.
Filter realization:
Figure 2-4-37 illustrates the direct realization of designed FIR filter, whereas figure 2-4-38 illustrates optimized realization structure of designed FIR filter which is based on the fact that all FIR filter coefficients are, for the sake of linear phase characteristic, symmetric about their middle element.
Figure 2-4-37. FIR filter direct realization
Figure 2-4-38. FIR filter optimized realization structure
2.4.5.3 Example 3
Step 1:
Type of filter – band-pass filter
Filte specifications:
-
- Sampling frequency – fs=16KHz;
-
- Passband cut-off frequency – fc1=2KHz, fc2=5KHz.
Step 2:
Method – filter design using Hamming window
Step 3:
Filter order is predetermined, Nf=12;
A total number of filter coefficients is larger by 1, i.e. N=Nf+1=13; and
Coefficients have indices between 0 and 12.
Step 4:
The Hamming window function coefficients are found via expression:
Step 5:
The ideal high-pass filter coefficients (ideal filter impulse response) are expressed as:
where M is the index of middle coefficient.
Normalized cut-off frequencies ωc1 and ωc2 can be calculated using expressions:
The values of coefficients (rounded to six digits) are obtained by combining the values of M, ωc1 and ωc2 with expression for the impulse response coefficients of the ideal band-pass filter:
Step 6:
The designed FIR filter coefficients are found via expression:
h[n] = w[n] * hd[n] ; 0 ≤ n ≤ 12
The FIR filter coefficients h[n] rounded to 6 digits are:
Step 7:
The filter order is predetermined.
There is no need to additionally change it.
Filter realization:
Figure 2-4-39 illustrates the direct realization of designed FIR filter, whereas figure 2-4-40 illustrates optimized realization structure of designed FIR filter which is based on the fact that all FIR filter coefficients are, for the sake of linear phase characteristic, symmetric about their middle elements.
Figure 2-4-39. FIR filter direct realization
Figure 2-4-40. FIR filter optimized realization structure
2.4.5.4 Example 4
Step 1:
Type of filter – band-stop filter
Filte specifications:
-
- Sampling frequency – fs=16000Hz; and
-
- Passband cut-off frequency – fc1=2KHz, fc2=6KHz.
Step 2:
Method – filter design using Hamming window
Step 3:
Filter order is predetermined, Nf=12;
A total number of filter coefficients is larger by 1, i.e. N=Nf+1=13; and
Coefficients have indices between 0 and 12.
Step 4:
The Bartlett-Hanning window function coefficients are found via expression:
Step 5:
The ideal high-pass filter coefficients (ideal filter impulse response) are expressed as:
where M is the index of middle coefficient.
Normalized cut-off frequencies ωc1 and ωc2 can be calculated using expressions:
The values of coefficients (rounded to six digits) are obtained by combining the values of M, ωc1 and ωc2 with expression for the impulse response coefficients of the ideal band-stop filter:
Step 6:
The designed FIR filter coefficients are found via expression:
h[n] = w[n] * hd[n] ; 0 ≤ n ≤ 12
The FIR filter coefficients h[n] rounded to 6 digits are:
Step 7:
The filter order is predetermined.
There is no need to additionally change it.
Filter realization:
Figure 2-4-41 illustrates the direct realization of designed FIR filter, whereas figure 2-4-42 illustrates optimized realization structure of designed FIR filter which is based on the fact that all FIR filter coefficients are, for the sake of linear phase characteristic, symmetric about their middle element.
Figure 2-4-41. FIR filter direct realization
Figure 2-4-42. FIR filter optimized realization structure
The first example (low-pass filter designed using Hamming window) explains the algorithm used to compute the needed filter order when it is unknown. The filter order can also be found using Kaiser window, after which the number of iterations, i.e. correction steps is reduced.
The forth example explains the way of designing a band-stop filter. As can be seen, the impulse response of the resulting filter contains large number of zero values, which results in reducing the number of multiplication operations in design process. These zeros appear in impulse response because of the stopband width which amounts to 0.5π = π/2.
If it is possible to specify the sampling frequency from a certain frequency range, you should tend to specify the value representing a multiple of the passband width. The number of zeros contained in an impulse response is larger in this case, whereas the number of multiplications, otherwise the most demanding operation in filtering process, is less.
In the given example, only 5 multiplication operations are performed in direct realization of a twelfth-order FIR filter, i.e. 3 multiplication operations in optimized realization structure.
2.4.6 Filter design using Bohman window
2.4.6.1 Example 1
Step 1:
Type of filter – low-pass filter
Filte specifications:
-
- Sampling frequency – fs=20KHz; and
-
- Passband cut-off frequency – fc=5KHz.
Step 2:
Method – filter design using Bohman window
Step 3:
Filter order is Nf=10;
A total number of filter coefficients is larger by 1, i.e. N=Nf+1=11; and
Coefficients have indices between 0 and 10.
Step 4:
The Bohman window function coefficients are found via expression:
Step 5:
The ideal low-pass filter coefficients (ideal filter impulse response) are expressed as:
where M is the index of middle coefficient.
Normalized cut-off frequency ωc may be computed using expression:
The values of coefficients (rounded to six digits) are obtained by combining the values of M and ωc with expression for the impulse response coefficients of the ideal low-pass filter:
Step 6:
The designed FIR filter coefficients are found via expression:
h[n] = w[n] * hd[n] ; 0 ≤ n ≤ 10
The FIR filter coefficients h[n] rounded to 6 digits are:
Step 7:
The filter order is predetermined.
There is no need to additionally change it.
Filter realization:
Figure 2-4-43 illustrates the direct realization of designed FIR filter, whereas figure 2-4-44 illustrates optimized realization structure of designed FIR filter which is based on the fact that all FIR filter coefficients are, for the sake of linear phase characteristic, symmetric about their middle element.
Figure 2-4-43. FIR filter direct realization
Figure 2-4-44. FIR filter optimized realization structure
2.4.6.2 Example 2
Step 1:
Type of filter – high-pass filter
Filte specifications:
-
- Sampling frequency – fs=22050Hz;
-
- Passband cut-off frequency – fc1=1.5KHz;
-
- Stopband cut-off frequency – fc2=4KHz; and
-
- Minimum stopband attenuation – 35dB.
Step 2:
Method – filter design using Bohman window
Step 3:
The needed filter order is determined via iteration.
It is necessary to specify the initial value of filter order that is to be changed as many times as needed. This value is specified according to the data contained in the table 2-4-2 below:
| WINDOW FUNCTION |
NORMALIZED LENGTH OF THE MAIN LOBE FOR N=20 |
TRANSITION REGION FOR N=20 |
MINIMUM STOPBAND ATTENUATION OF WINDOW FUNCTION |
MINIMUM STOPBAND ATTENUATION OF DESIGNED FILTER |
|---|
| Rectangular |
0.1π |
0.041π |
13 dB |
21 dB |
| Triangular (Bartlett) |
0.2π |
0.11π |
26 dB |
26 dB |
| Hann |
0.21π |
0.12π |
31 dB |
44 dB |
| Bartlett-Hanning |
0.21π |
0.13π |
36 dB |
39 dB |
| Hamming |
0.23π |
0.14π |
41 dB |
53 dB |
| Bohman |
0.31π |
0.2π |
46 dB |
51 dB |
| Blackman |
0.32π |
0.2π |
58 dB |
75 dB |
| Blackman-Harris |
0.43π |
0.32π |
91 dB |
109 dB |
Table 2-4-2. Comparison of window functions
According to the specifications for the transition region of required filter, it is possible to compute cut-off frequencies:
The required transition region is:
The transition region of the filter to be designed is somewhat wider than that of the filter given in table 2-4-2. For the first iteration, during filter design process, the filter order can be lower.
Unlike the low-pass FIR filter, the high-pass FIR filter must be of even order. The same applies to band-pass and band-stop filters. It means that filter order can be changed in odd steps. The smallest change is ±2. In this case, the filter order, comparing to that from the table (20), can be decreased by 2 for the purpose of defining initial value.
Filter order is Nf=18;
A total number of filter coefficients is larger by 1, i.e. N=Nf+1=19; and
Coefficients have indices between 0 and 18.
Step 4:
The coefficients of Bohman window are found via expression:
Step 5:
The ideal high-pass filter coefficients (ideal filter impulse response) are expressed as:
where M is the index of middle coefficient.
Normalized cut-off frequency ωc is equal to passband cut-off frequency:
The values of coefficients (rounded to six digits) are obtained by combining the values of M and ωc with expression for the impulse response coefficients of the ideal high-pass filter:
Step 6:
The designed FIR filter coefficients are found via expression:
h[n] = w[n] * hd[n] ; 0 ≤ n ≤ 18
The FIR filter coefficients h[n] rounded to 6 digits are:
Step 7:
Analyse in the frequency domain is performed using the
Filter Designer Tool program.
Figure 2-4-45. Frequency characteristics of the resulting filter
Figure 2-4-45 illustrates the frequency characteristic of the resulting filter. It is obtained in the
Filter Designer Tool program. As seen, the resulting filter satisfies the required specifications. The attenuation at the frequency of 1500Hz amounts to 37.04dB only, which is more than enough. However, the final objective when designing a filter is to find a minimum filter order that satisfies the filter specifications.
Since the filter order must be changed by an even number, the specified value is -2. The filter order is decreased by 2. The whole process of designing filters is repeated from the step 3 on.
Step 3:
Filter order is Nf=16;
A total number of filter coefficients is larger by 1, i.e. N=Nf+1=17; and
Coefficients have indices between 0 and 16.
Step 4:
The coefficients of Bohman window are found via expression:
Step 5:
The ideal high-pass filter coefficients (ideal filter impulse response) are expressed as:
where M is the index of middle coefficient.
Normalized cut-off frequency ωc is equal to the passband cut-off frequency:
The values of coefficients (rounded to six digits) are obtained by combining the values of M and ωc with expression for the impulse response coefficients of the ideal high-pass filter:
Step 6:
The designed FIR filter coefficients are found via expression:
h[n] = w[n] * hd[n] ; 0 ≤ n ≤ 16
The FIR filter coefficients h[n] rounded to 6 digits are:
Step 7:
Analyse in the frequency domain is performed using the Filter Designer Tool program.
Figure 2-4-46. Frequency characteristic of the resulting filter
Figure 2-4-46 illustrates the frequency characteristic of the resulting filter. The figure is obtained in the
Filter Designer Tool program. As seen, the resulting filter satisfies the required specifications. The objective is to find the minimum filter order. Since the attenuation is close to the required attenuation, the correct order is probably 16. However, it is necessary to check it.
Since the filter order must be changed by an even number, the specified value is -2. The filter order is decreased by 2, therefore. The whole process of designing filter is repeated from the step 3 on.
Step 3:
Filter order is predetermined, Nf=14;
A total number of filter coefficients is larger by 1, i.e. N=Nf+1=15; and
Coefficients have indices between 0 and 14.
Step 4:
The coefficients of Bohman window are found via expression:
Step 5:
The ideal high-pass filter coefficients (ideal filter impulse response) are expressed as:
where M is the index of middle coefficient.
Normalized cut-off frequency ωc is equal to passband cut-off freqency:
The values of coefficients (rounded to six digits) are obtained by combining the values of M and ωc with expression for the impulse reaponse coefficients of the ideal high-pass filter:
Step 6:
The designed FIR filter coefficients are found via expression:
h[n] = w[n] * hd[n] ; 0 ≤ n ≤ 14
The FIR filter coefficients h[n] rounded to 6 digits are:
Step 7:
Analyse in the frequency domain is performed using the Filter Designer Tool program.
Figure 2-4-47. Frequency characteristic of the resulting filter
Figure 2-4-47 illustrates the frequency characteristic of the resulting filter. The figure is obtained in the Filter Designer Tool program. As seen, the resulting filter doesn’t satisfy the required specifications. The attenuation at the frequency of 1500KHz amounts to 26.24dB only, which is not sufficient. The previous value (Nf=16) represents the minimum FIR filter order that satisfies the given specifications.
The filter order is Nf=16, whereas impulse response of the resulting filter is as follows:
Filter realization:
Figure 2-4-48 illustrates the direct realization of designed FIR filter, whereas figure 2-4-49 illustrates optimized realization structure of designed FIR filter which is based on the fact that all FIR filter coefficients are, for the sake of linear phase characteristic, symmetric about their middle element.
Figure 2-4-48. FIR filter direct realization
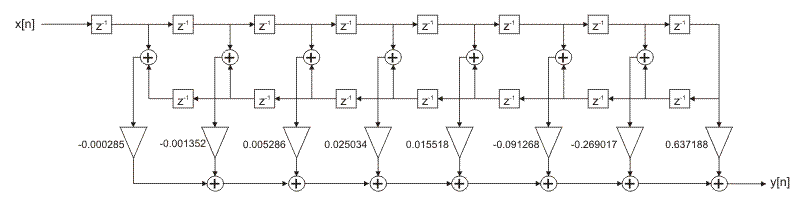
Figure 2-4-49. FIR filter optimized realization structure
2.4.6.3 Example 3
Step 1:
Type of filter – band-pass filter
Filte specifications:
-
- Sampling frequency – fs=44100Hz; and
-
- Passband cut-off frequency – fc1=4KHz, fc2=15025Hz.
Step 2:
Method – filter design using Bohman window
Step 3:
Filter order is predetermined, Nf=12;
A total number of filter coefficients is larger by 1, i.e. N=Nf+1=13; and
Coefficients have indices between 0 and 12.
Step 4:
The coefficients of Bohman window are found via expression:
Step 5:
The ideal high-pass filter coefficients (ideal filter impulse response) are expressed as:
where M is the index of middle coefficient.
Normalized cut-off frequencies ωc1 and ωc2 can be calculated using expressions:
The values of coefficients (rounded to six digits) are obtained by combining the values of M, ωc1 and ωc2 with expression for the impulse response coefficients of the ideal band-pass filter:
Step 6:
The coefficients of designed FIR filter are found via expression:
h[n] = w[n] * hd[n] ; 0 ≤ n ≤ 12
The FIR filter coefficients h[n] rounded to 6 digits are:
Step 7:
The filter order is predetermined.
There is no need to additionally change it.
Filter realization:
Figure 2-4-50 illustrates the direct realization of designed FIR filter, whereas figure 2-4-51 illustrates optimized realization structure of designed FIR filter which is based on the fact that all FIR filter coefficients are, for the sake of linear phase characteristic, symmetric about their middle element.
Figure 2-4-50. FIR filter direct realization
Figure 2-4-51. FIR filter optimized realization structure
2.4.6.4 Example 4
Step 1:
Type of filter – band-stop filter
Filte specifications:
-
- Sampling frequency – fs=16000Hz; and
-
- Passband cut-off frequency – fc1=2KHz, fc2=6KHz.
Step 2:
Method – filter design using Bohman window
Step 3:
Filter order is predetermined, Nf=12;
A total number of filter coefficients is larger by 1, i.e. N=Nf+1=13; and
Coefficients have indices between 0 and 12.
Step 4:
The coefficients of Bohman window are found via expression:
Step 5:
The ideal high-pass filter coefficients (ideal filter impulse response) are expressed as:
where M is the index of middle coefficient.
Normalized cut-off frequencies ωc1 and ωc2 can be calculated using expressions:
The values of coefficients (rounded to six digits) are obtained by combining the values of M, ωc1 and ωc2 with expression for the impulse response coefficients of the ideal band-stop filter:
Step 6:
The designed FIR filter coefficients are found via expression:
h[n] = w[n] * hd[n] ; 0 ≤ n ≤ 12
The FIR filter coefficients h[n] rounded to 6 digits are:
Step 7:
The filter order is predetermined.
There is no need to additionally change it.
Filter realization:
Figure 2-4-52 illustrates the direct realization of designed FIR filter, whereas figure 2-4-53 illustrates optimized realization structure of designed FIR filter which is based on the fact that all FIR filter coefficients are, for the sake of linear phase characteristic, symmetric about their middle element.
Figure 2-4-52. FIR filter direct realization
Figure 2-4-53. FIR filter optimized realization structure
2.4.7 Filter design using Blackman window
2.4.7.1 Example 1
Step 1:
Type of filter – low-pass filter
Filte specifications:
-
- Sampling frequency – fs=44100KHz;
-
- Passband cut-off frequency – fc=15KHz; and
-
- Attenuation of 0dB at 0Hz – 0dB.
Step 2:
Method –Filter design using Blackman window
Step 3:
Filter order is predetermined, Nf=12;
A total number of filter coefficients is larger by 1, i.e. N=Nf+1=13;
Coefficients have indices between 0 and 12.
Step 4:
The coefficients of Blackman window are found via expression:
Step 5:
The ideal low-pass filter coefficients (ideal filter impulse response) are expressed as:
where M is the index of middle coefficient.
Normalized cut-off frequency ωc can be computed using expression:
The values of coefficients are obtained (rounded to six digits) by combining the values of M and ωc with expression for the impulse response coefficients of the ideal low-pass filter:
Step 6:
The designed FIR filter coefficients are found via expression:
h[n] = w[n] * hd[n] ; 0 ≤ n ≤ 12
The FIR filter coefficients h[n] rounded to 6 digits are:
The resulting coefficients must be scaled in order to provide attenuation of 0dB at 0Hz. In order to provide attenuation of 0 dB, the following condition must be met:
The sum of the previously obtained coefficients is:
As the sum is greater than one, it is necessary to divide all coefficients of the impulse response by 1.000274. After division, these coefficients have the following values:
The sum of scaled coefficients is equal to 1, which means that attenuation at 0Hz frequency amounts to 0dB. Note that these coefficients cannot be used in designing a FIR filter safe from filtering overflow. In order to prevent a filtering overflow from occuring it is necessary to satisfy the condition below:
The resulting filter doesn’t meet this condition. Negative coefficients in impulse response make that both conditions cannot be met. The sum of apsolute values of coefficients in the resulting filter is:
The sum of coefficients apsolute values before scaling amounts to 1.37001 (1.369636⋅1.000274). After scaling, it is somewhat less, so it is less likely that an overflow occurs. In such cases, possible filtering overflows are not dangerous. Namely, most processors containing hardware multipliers (which is almost necessary for filtering) have registers with extended band. In this case, it is far more important to faithfully transmit a direct signal to a FIR filter output.
Step 7:
The filter order is predetermined.
There is no need to additionally change it.
Filter realization:
Figure 2-4-54 illustrates the direct realization of designed FIR filter, whereas figure 2-4-55 illustrates optimized realization structure of designed FIR filter which is based on the fact that all FIR filter coefficients are, for the sake of linear phase characteristic, symmetric about their middle element.
Figure 2-4-54. FIR filter direct realization
Figure 2-4-55. FIR filter optimized realization structure
2.4.7.2 Example 2
Step 1:
Type of filter – high-pass filter
Filte specifications:
-
- Sampling frequency – fs=22050Hz;
-
- Passband cut-off frequency – fc=4KHz;
-
- Prevention of possible filtering overflows.
Step 2:
Method –filter design using Blackman window
Step 3:
Filter order is Nf=12;
A total number of filter coefficients is larger by 1, i.e. N=Nf+1=13;
Coefficients have indices between 0 and 12.
Step 4:
The coefficients of Blackman window function are found via:
Step 5:
The ideal high-pass filter coefficients (ideal filter impulse response) are expressed as:
where M is the index of middle coefficient.
Normalized cut-off frequency ωc can be computed using expression:
The values of coefficients (rounded to six digits) are obtained by combining the values of M and ωc with expression for the impulse response coefficients of the ideal high-pass filter:
Step 6:
The designed FIR filter coefficients are found via expression:
h[n] = w[n] * hd[n] ; 0 ≤ n ≤ 12
The FIR filter coefficients h[n] rounded to 6 digits are:
In order to prevent filtering overflow, the following condition must be met:
The sum of absolute values of the resulting FIR filter coefficients is:
The obtained coefficients must be scaled (divided) by 1.34807. After that, their values are:
Step 7:
The filter order is predetermined.
There is no need to additionally change it.
Filter realization:
Figure 2-4-56 illustrates the direct realization of designed FIR filter, whereas figure 2-4-57 illustrates optimized realization structure of designed FIR filter which is based on the fact that all FIR filter coefficients are, for the sake of linear phase characteristic, symmetric about their middle element.
Figure 2-4-56. FIR filter direct realization
Figure 2-4-57. FIR filter optimized realization structure
2.4.7.3 Example 3
Step 1:
Type of filter – band-pass filter
Filte specifications:
-
- Sampling frequency – fs=44100Hz;
-
- Passband cut-off frequency – fc1=4KHz, fc2=15025Hz;
-
- Prevention of possible filtering overflow.
Step 2:
Method –filter design using Blackman window
Step 3:
Filter order is predetermined, Nf=12;
A total number of filter coefficients is larger by 1, i.e. N=Nf+1=13;
Coefficients have indices between 0 and 12.
Step 4:
The coefficients of Blackman window function are found via expression:
Step 5:
The ideal high-pass filter coefficients (ideal filter impulse response) are expressed as:
where M is the index of middle coefficient.
Normalized cut-off frequencies ωc1 and ωc2 can be computed using expressions:
The values of coefficients (rounded to six digits) are obtained by combining the values of M, ωc1 and ωc2 with expression for the impulse response coefficients of the ideal band-pass filter:
Step 6:
The designed FIR filter coefficients are found via expression:
h[n] = w[n] * hd[n] ; 0 ≤ n ≤ 12
The FIR filter coefficients h[n] rounded to 6 digits are:
In order to prevent filtering overflows, the following condition must be met:
The sum of absolute values of the resulting FIR filter coefficients is:
The obtained coefficients must be scaled (divided) by 1.102056. After this, their values are:
Step 7:
The filter order is predetermined.
There is no need to additionally change it.
Filter realization:
Figure 2-4-58 illustrates the direct realization of designed FIR filter, whereas figure 2-4-59 illustrates optimized realization structure of designed FIR filter which is based on the fact that all FIR filter coefficients are, for the sake of linear phase characteristic, symmetric about their middle element.
Figure 2-4-58. FIR filter direct realization
Figure 2-4-59. FIR filter optimized realization structure
2.4.7.4 Example 4
Step 1:
Type of filter – band-stop filter
Filte specifications:
-
- Sampling frequency – fs=16000Hz;
-
- Passband cut-off frequencies – fc1=2KHz, fc2=6KHz;
-
- Prevention of possible filtering overflows.
Step 2:
Method – filter design using Blackman window
Step 3:
Filter order is predetermined, Nf=12;
A total number of filter coefficients is larger by 1, i.e. N=Nf+1=13;
Coefficients have indices between 0 and 12.
Step 4:
The coefficients of Blackman window are found via expression:
Step 5:
The ideal high-pass filter coefficients (ideal filter impulse response) are expressed as:
where M is the index of middle coefficient.
Normalized cut-off frequencies ωc1 and ωc2 can be computed using expressions:
The values of coefficients (rounded to six digits) are obtained by combining the values of M, ωc1 and ωc2 with expression for the impulse response coefficients of the ideal band-stop filter:
Step 6:
The designed FIR filter coefficients are found via expression:
h[n] = w[n] * hd[n] ; 0 ≤ n ≤ 12
The FIR filter coefficients h[n] rounded to 6 digits are:
In order to prevent filtering overflows, the following condition must be met:
The sum of absolute values of the resulting FIR filter coefficients is:
The obtained coefficients must be scaled (divided) by 0.90107. After this, their values are:
Step 7:
The filter order is predetermined.
There is no need to additionally change it.
Filter realization:
Figure 2-4-60 illustrates the direct realization of designed FIR filter, whereas figure 2-4-61 illustrates optimized realization structure of designed FIR filter which is based on the fact that all FIR filter coefficients are, for the sake of linear phase characteristic, symmetric about their middle element.
Figure 2-4-60. FIR filter direct realization
Figure 2-4-61. FIR filter optimized realization structure
2.4.8 Filter design using Blackman-Harris window
2.4.8.1 Example 1
Step 1:
Type of filter –low-pass filter
Filte specifications:
-
- Sampling frequency – fs=44100KHz;
-
- Passband cut-off frequency – fc=15KHz;
-
- Attenuation of 0dB at 0Hz.
Step 2:
Method –filter design usng Blackman-Harris window
Step 3:
Filter order is predetermined, Nf=12;
A total number of filter coefficients is larger by 1, i.e. N=Nf+1=13; and
Coefficients have indices between 0 and 12.
Step 4:
The coefficients of Blackman-Harris window are found via expression:
Step 5:
The ideal high-pass filter coefficients (ideal filter impulse response) are expressed as:
where M is the index of middle coefficient.
Normalized cut-off frequency ωc may be calculated using expression:
The values of coefficients (rounded to six digits) are obtained by combining the values of M and ωc with expression for the impulse response coefficients of the ideal low-pass filter:
Step 6:
The designed FIR filter coefficients are found via expression:
h[n] = w[n] * hd[n] ; 0 ≤ n ≤ 12
The FIR filter coefficients h[n] rounded to 6 digits are:
The resulting coefficients must be scaled in order to provide attenuation of 0dB at 0Hz. To provide 0 dB attenuation, the following condition must be met:
The sum of the previously obtained coefficients is:
As the sum is greater than one, it is necessary to divide all the impulse response coefficients by 0.977947. After this, the values of these coefficients are:
The sum of scaled coefficients is equal to 1, which means that attenuation at 0Hz frequency amounts to 0dB. Note that these coefficients cannot be used in designing a FIR filter safe from filtering overflow. In order to prevent a filtering overflow from occuring it is necessary to satisfy the condition below:
The resulting filter doesn’t meet this condition. Negative coefficients in impulse response indicate that both conditions cannot be met. The sum of apsolute values of coefficients in the resulting filter is:
The sum of coefficients apsolute values before scaling amounts to 1.37001 (1.369636⋅1.000274). After scaling, the sum of coefficients apsolute values is somewhat less, so it is less possible that an overflow occurs. In such cases, possible filtering overflows are not dangerous. Namely, most processors containing hardware multipliers (which is almost necessary for filtering) have registers with extended band. In this case, it is far more important to faithfully transmit a direct signal to a FIR filter output.
Step 7:
The filter order is predetermined.
There is no need to additionally change it.
Filter realization:
Figure 2-4-62 illustrates the direct realization of designed FIR filter, whereas figure 2-4-63 illustrates optimized realization structure of designed FIR filter which is based on the fact that all FIR filter coefficients are, for the sake of linear phase characteristic, symmetric about their middle element.
Figure 2-4-62. FIR filter
Figure 2-4-63. Optimized FIR filter design
2.4.8.2 Example 2
Step 1:
Type of filter – high-pass filter
Filte specifications:
-
- Sampling frequency – fs=22050Hz;
-
- Passband cut-off frequency – fc=4KHz;
-
- Prevention of filtering overflows.
Step 2:
Method – filter design using Blackman-Harris window
Step 3:
Filter order is Nf=12;
A total number of filter coefficients is larger by 1, i.e. N=Nf+1=13; and
Coefficients have indices between 0 and 12.
Step 4:
The coefficients of Blackman-Harris window are found via:
Step 5:
The ideal high-pass filter coefficients (ideal filter impulse response) are expressed as:
where M is the index of middle coefficient.
Normalized cut-off frequency ωc can be computed using expression:
The values of coefficients (rounded to six digits) are obtained by combining the values of M and ωc with the expression for the impulse response coefficients of the ideal high-pass filter:
Step 6:
The designed FIR filter coefficients are found via expression:
h[n] = w[n] * hd[n] ; 0 ≤ n ≤ 12
The FIR filter coefficients h[n] rounded to 6 digits are:
In order to prevent filtering overflow, the following condition must be met:
The sum of absolute values of the resulting FIR filter coefficients is:
The obtained coefficients must be scaled (divided) by 1.397791. After this, their values are:
Step 7:
The filter order is predetermined.
There is no need to additionally change it.
Filter realization:
Figure 2-4-64 illustrates the direct realization of designed FIR filter, whereas figure 2-4-65 illustrates optimized realization structure of designed FIR filter which is based on the fact that all FIR filter coefficients are, for the sake of linear phase characteristic, symmetric about their middle element.
Figure 2-4-64. FIR filter direct realization
Figure 2-4-65. Optimized FIR filter design
2.4.8.3 Example 3
Step 1:
Type of filter –band-pass filter
Filter specification:
-
- Sampling frequency – fs=44100Hz;
-
- Passband cut-off frequencies – fc1=4KHz, fc2=15025Hz; and
-
- Prevention of possible filtering overflows.
Step 2:
Method – filter design using Blackman-Harris window
Step 3:
Filter order is predetermined, Nf=12;
A total number of filter coefficients is larger by 1, i.e. N=Nf+1=13; and
Coefficients have indices between 0 and 12.
Step 4:
The coefficients of Blackman-Harris window are found via expression:
Step 5:
The ideal high-pass filter coefficients (ideal filter impulse response) are expressed as:
where M is the index of middle coefficient.
Normalized cut-off frequencies ωc1 and ωc2 can be computed using expressions:
The values of coefficients (rounded to six digits) are obtained by combining the values of M, ωc1 and ωc2 with expression for the impulse response coefficients of the ideal band-pass filter:
Step 6:
The designed FIR filter coefficients are found via expression:
h[n] = w[n] * hd[n] ; 0 ≤ n ≤ 12
The FIR filter coefficients h[n] rounded to 6 digits are:
Step 7:
The filter order is predetermined.
There is no need to additionally change it.
Filter reaization:
Figure 2-4-66 illustrates the direct realization of designed FIR filter, whereas figure 2-4-67 illustrates optimized realization structure of designed FIR filter which is based on the fact that all FIR filter coefficients are, for the sake of linear phase characteristic, symmetric about their middle element.
Figure 2-4-66. FIR filter direct realization
Figure 2-4-67. Optimized FIR filter design
2.4.8.4 Example 4
Step 1:
Type of filter – band-stop filter
Filter specification:
-
- Sampling frequency – fs=16000Hz;
-
- Passband cut-off frequency – fc1=2KHz, fc2=6KHz; and
-
- Prevention of possible filtering overflows.
Step 2:
Method – filter design using Blackman-Harris window
Step 3:
Filter order is predetermined, Nf=20;
A total number of filter coefficients is larger by 1, i.e. N=Nf+1=21; and
Coefficients have indices between 0 and 20.
Step 4:
The coefficients of Blackman-Harris window are found via expression:
Step 5:
The ideal high-pass filter coefficients (ideal filter impulse response) are expressed as:
where M is the index of middle coefficient.
Normalized cut-off frequencies ωc1 and ωc2 can be computed using expressions:
The values of coefficients (rounded to six digits) are obtained by combining the values of M, ωc1 and ωc2 with expression for the impulse response coefficients of the ideal band-stop filter:
Step 6:
The designed FIR filter coefficients are found via expression:
h[n] = w[n] * hd[n] ; 0 ≤ n ≤ 20
The FIR filter coefficients h[n] rounded to 6 digits are:
In order to prevent filtering overflows, the following condition must be met:
The sum of absolute values of the resulting FIR filter coefficients is:
The obtained coefficients must be scaled (divided) by 1.12232. After this, their values are:
Step 7:
The filter order is predetermined.
There is no need to additionally change it.
Filter realization:
Figure 2-4-68 illustrates the direct realization of designed FIR filter, whereas figure 2-4-69 illustrates optimized realization structure of designed FIR filter which is based on the fact that all FIR filter coefficients are, for the sake of linear phase characteristic, symmetric about their middle element.
This FIR filter is an excellent example showing the importance of the sampling frequency. It is specified to give the passband amounting to 0.5π. This causes most impulse response coefficients of the resulting FIR filter to be zeros. It further makes the filter realization structure simpler. As for optimized FIR filter design, there are only 4 multiplications, even though the filter is of 20th order. Unfortunatelly, the buffer length cannot be minimized. It is fixed and corresponds to the filter order. However, it is possible to affect design complexity, whether it is hardware or software implementation.
Figure 2-4-68. FIR filter direct realization
Figure 2-4-69. Optimized FIR filter design












































































































































































































































































































































