This chapter discusses various IIR filter design methods. The four standard types of filters are used here:

 

• • low-pass filter;

 

• • high-pass filter;

 

• • band-pass filter; and

 

• • band-stop filter.

The design method used here is known as bilinear transformation.

The IIR filter design process can be split into several steps described in Chapter 3.2.5 Designing IIR filters by bilinear transformation. These are:
 

1. 1. Defining filter specifications;

 

1. 1. Specifying the type of analog prototype filter;

 

1. 1. Computing the filter order according to the filter specifications and specified analog prototype filter;

 

1. 1. Computing the transfer function of reference analog prototype filter;

 

1. 1. Transformation into analog filter by range scaling;

 

1. 1. Transformation into digital filter by bilinear transformation; and

 

1. 1. If the resulting filter doesn’t satisfy the given specifications or if it is possible to decrease the filter order, then it is necessary to do it. The specified filter order is increased or decreased according to needs, and steps 4, 5 and 6 are repeated after that as many times as needed.

Some steps are skipped in some cases. If the filter order is known, step 3 is skipped. If the type of reference analog prototype filter is predetermined, step 2 is skipped.

In every given example, the IIR filter design process will be described through these steps in order to make it easier for you to observe similarities and differencies between various design methodes, analog prototype filters and design of various types of filters as well.

Figure 3-6-1 illustrates the design steps along with input and output data for each of them.  
The first block refers to design of reference analog prototype filter of appropriate order. The output data is a reference analog prototype filter transfer function Ha(s). Regardless of the type of reference analog prototype filter in use, the transfer function is given by:
where:
H0 is a constant;
zk is the k-th zero of the reference analog prototype filter transfer function;
M is a number of zeros of the reference analog prototype filter transfer function;
pk is the k-th pole of the reference analog prototype filter transfer function; and
N is a number of poles of the reference analog prototype filter transfer function and filter order as well.

Reference analog prototype filter is always a low-pass filter. The next step is the transformation into an analog filter of appropriate type. The expression used to transform the reference analog prototype filter transfer function depends on the type of filter that needs to be obtained. The final result is the transfer function H(s) given by:
where:
H0 is a constant;
zk is the k-th zero of the reference analog prototype filter transfer function;
M is a number of zeros of the reference analog prototype filter transfer function;
pk is the k-th pole of the reference analog prototype filter transfer function; and
N is a number of poles of the reference analog prototype filter transfer function and filter order as well.

As seen, the transfer functions of reference analog prototype filter and analog filter are very similar. They differ only in the value of constant H0, the values of the transfer function poles and zeros zk and pk as well as in the number of transfer function zeros M. The filter order is the same if the analog filter is a low-pass or high-pass filter, whereas it is different if the analog filter is a band-pass or band-stop filter. In the later case, the analog filter order (N) is twice that of the reference analog prototype filter.

The next step is the transformation into appropriate digital IIR filter using bilinear transformation given by expression:
Filter Designer Tool is used for testing and analysing the resulting IIR filters in this chapter. All data are calculated with the accuracy of 4 decimal digits, which is sufficient for most examples.

3.6.1 Filter design using Butterworth filter

 

3.6.1.1 Example 1

Step 1:

Type of filter – low-pass filter
Filter specifications:
 

• • Filter order – N=2;

 

• • Sampling frequency – fs=20KHz;

 

• • Passband cut-off frequency – fc=2.5KHz; and

 

• • Minimum stopband attenuation – ap=40dB.

Step 2:

Method- filter design using Butterworth reference analog prototype filter.

Step 3:

Filter order is predetermined, N=2.

Step 4:

The Butterworth reference prototype filter transfer function has no zeros, only poles. These can be computed via expression:
As N = 2, the values of poles are:
The reference analog prototype filter transfer function is:
Step 5:

First it is necessary to compute the analog prototype filter cut-off frequency Ωc.
The analog filter transfer function is obtained from the reference analog prototype filter transfer function using expression:
As the Butterworth reference prototype filter has no zeros, the expression for transfer function is simpler:    
Step 6:

The transformation into a digital filter through bilinear transformation:
Generally, substituting the complex variable s into the expression for analog filter transfer function, the following is obtained:
where:
zk are the zeros of analog filter transfer function; and
pk are the poles of analog filter transfer function.

This general expression can be written in a simpler way in this example:    
A more condensed form of the previous expression is:    
The result is the IIR filter transfer function.

Step 7:

The filter order is predetermined.
There is no need to additionally change it.

Filter realization:

Figure 3-6-2 illustrates the direct realization of designed IIR filter, whereas Figure 3-6-3 illustrates the frequency response of the filter obtained using Filter Designer Tool.          

3.6.1.2 Example 2

Step 1:

Type of filter – high-pass filter
Filter specifications:
 

• • Filter order – N=3;

 

• • Sampling frequency – fs=20KHz;

 

• • Passband cut-off frequency – fc=5KHz; and

 

• • Minimum stopband attenuation – ap=40dB.

Step 2:

Method- filter design using Butterworth reference analog prototype filter

Step 3:

Filter order is predetermined, N = 3.

Step 4:

The Butterworth reference prototype filter transfer function has no zeros, only poles. These can be computed via expression:
As N = 3, the values of poles are:
The reference analog prototype filter transfer function is:
Step 5:

First it is necessary to compute the analog prototype filter cut-off frequency Ωc.
The analog filter transfer function is obtained from the reference analog prototype filter transfer function using expression:
As the Butterworth reference prototype filter has no zeros, the expression for transfer function is simpler:    
Step 6:

The transformation into a digital filter through bilinear transformation:
Generally, substituting the complex variable s into the expression for analog filter transfer function, the following is obtained:
where:
zk are the zeros of analog filter transfer function; and
pk are the poles of analog filter transfer function.

This general expression can be written in a simpler way in this example:
A more condensed form of the previous expression is:
The result is the IIR filter transfer function.

Step 7:

The filter order is predetermined.
There is no need to additionally change it.

Filter realization:

Figure 3-6-4 illustrates the direct realization of designed IIR filter.          

3.6.1.3 Example 3

Step 1:

Type of filter – band-pass filter
Filter specifications:
 

• • Filter order – N=4;

 

• • Sampling frequency – fs=20KHz; and

 

• • Passband cut-off frequency – fc1=4KHz, fc2=6KHz.

Step 2:

Method - filter design using Butterworth reference analog prototype filter

Step 3:

Filter order is predetermined, N = 4.

Step 4:

The Butterworth reference prototype filter transfer function has no zeros, only poles. These can be computed via expression:
When designing an IIR band-pass filter, the reference prototype filter order is half that of the required IIR filter order. In this example for N=4, the order of reference prototype filter is 2, so the values of poles are:
The reference analog prototype filter transfer function is:
Step 5:

First it is necessary to compute the analog prototype filter cut-off frequency Ωc.    
The analog filter transfer function is obtained from the reference analog prototype filter transfer function using expression:
As the Butterworth reference prototype filter has no zeros, the expression for transfer function is simpler:    
Step 6:

The transformation into a digital filter through bilinear transformation:
Generally, by substituting the complex variable s into the expression for analog filter transfer function, the following is obtained:
where:
zk are the zeros of analog filter transfer function; and
pk are the poles of analog filter transfer function.

In this example, the general expression can be written in a simpler way:
A more condensed form of the previous expression is:
The result is the IIR filter transfer function.

Step 7:

Filter order is predetermined.
There is no need to additionally change it.

Filter realization:

Figure 3-6-6 illustrates the direct realization of designed IIR filter.          

3.6.1.4 Example 4

Step 1:

Type of filter – band-stop filter
Filter specifications:
 

• • Filter order – N=4;

 

• • Sampling frequency – fs=20KHz; and

 

• • Passband cut-off frequency – fc1=3000Hz, fc2=3300Hz.

Step 2:

Method - filter design using Butterworth reference analog prototype filter.

Step 3:

Filter order is predetermined, N = 4.

Step 4:

The Butterworth reference prototype filter transfer function has no zeros, only poles. These can be computed via expression:
When designing an IIR band-stop filter, the reference prototype filter order is half that of the required IIR filter order. In this example for N = 4, the order of reference prototype filter is 2, so the values of poles are:
The reference analog prototype filter transfer function is:
Step 5:

First it is necessary to compute the analog prototype filter cut-off frequency Ωc.
The analog filter transfer function is obtained from the reference analog prototype filter transfer function using expression:
As the Butterworth reference prototype filter has no zeros, the expression for transfer function is simpler:  
Step 6:

The transformation into a digital filter through bilinear transformation:
Generally, by substituting the complex variable s into the expression for analog filter transfer function, the following is obtained:
where:
zk are the zeros of analog filter transfer function; and
pk are the poles of analog filter transfer function.

In this example, the general expression can be written in a simpler way:
A more condensed form of the previous expression is:
The result is the IIR filter transfer function.

Step 7:

Filter order is predetermined.
There is no need to additionally change it.

Filter realization:

Figure 3-6-8 illustrates the direct realization of designed IIR filter.          

3.6.2 Filter design using Chebyshev filter

 

3.6.2.1 Example 1

Step 1:

Type of filter – low-pass filter
Filter specifications:
 

• • Sampling frequency – fs=44100Hz;

 

• • Passband cut-off frequency– fc1=15KHz;

 

• • Stopband cut-off frequency – fc2=18KHz;

 

• • Maximum passband attenuation – ap=1dB; and

 

• • Minimum stopband attenuation – as=40dB.

Step 2:

Method - filter design using Chebyshev reference analog prototype filter

Step 3:

Filter order is not pre-determined, so it is necessary to choose an initial solution from which iterative method starts. The solution is redefined progressively until some pre-determined requirements are satisfied. Let’s assume that the initial filter order is 4.

Step 4:

The Chebyshev reference prototype filter transfer function has no zeros, only poles. These can be computed via expression:
As N = 4, the values of poles are:
The Chebyshev filter transfer function is expressed as:
In this case, the value of constant A0 is:

A0 = 0.2457

so that the Chebyshev reference analog prototype filter transfer function is:
Step 5:

First it is necessary to compute the analog prototype filter cut-off frequency Ωc.
The analog filter transfer function is obtained from the reference analog prototype filter transfer function using expression:
As the Chebyshev reference prototype filter has no zeros, the expression for transfer function is simpler:    
Step 6:

The transformation into a digital filter through bilinear transformation:
Generally, by substituting the complex variable s into the expression for analog filter transfer function, the following is obtained:
where:
zk are the zeros of analog filter transfer function; and
pk are the poles of analog filter transfer function.

This general expression can be written in a simpler way in this example:
A more condensed form of the previous expression is:    
The result is the IIR filter transfer function.

Step 7:

By analyzing the resulting filter using Filter Designer Tool, it is obvious that the attenuation amounting to 31.2dB approximately at the frequency of 18KHZ is not sufficient. The frequency characteristic of the resulting digital filter is illustrated in Figure 3-6-10 below.  
It is necessary to additionally redefine the filter order until the predefined requirements are satisfied. The filter order is incremented by 1 and is 5 therefore. All steps starting with step 3 are iterated.

Step3:

The filter order is incremented in the second iteration. A new filter order is 5.

Step 4:

The Chebyshev reference prototype filter transfer function has no zeros, only poles. These can be computed via expression:
As N = 5, the values of poles are:
The Chebyhsev filter transfer function is expressed as:
In this case, the value of constant A0 is:

A0 = - 0.1228

so the Chebyshev reference analog prototype filter transfer function is:
Step 5:

First it is necessary to compute the analog prototype filter cut-off frequency Ωc.
The analog filter transfer function is obtained from the reference analog prototype filter transfer function using expression:
As the Chebyshev reference prototype filter has no zeros, the expression for transfer function is simpler:    
Step 6:

The transformation into a digital filter through bilinear transformation:
Generally, substituting the complex variable s into the expression for analog filter transfer function, the following is obtained:
where:
zk are the zeros of analog filter transfer function; and
pk are the poles of analog filter transfer function.

This general expression can be written in a simpler way in this example:
A more condensed form of the previous expression is:
The result is the IIR filter transfer function.

Step 7:

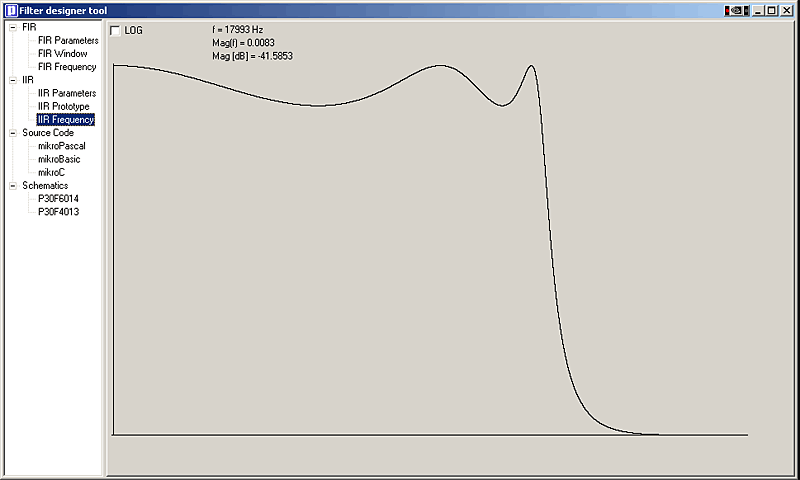
By analyzing the resulting filter using Filter Designer Tool, it is obvious that the attenuation amounting to 41.6dB approximately at the frequency of 18KHZ is not sufficient. The frequency characteristic of the resulting digital filter is illustrated in Figure 3-6-11 below.  
It is not necessary to further increase the filter order as this one is appropriate. Sometimes more iterations are needed to determine the filter order. The whole procedure is the same, only it takes more time.

Filter realization:

Figure 3-6-12 illustrates the direct realization of designed IIR filter, whereas Figure 3-6-13 illustrates the frequency characteristic of the filter obtained using Filter Designer Tool.          

3.6.1.2 Example 2

Step 1:

Type of filter – high-pass filter
Filter specifications:
 

• • Filter order – N = 3;

 

• • Sampling frequency – fs = 20KHz;

 

• • Passband cut-off frequency – fc = 5KHz; and

 

• • Maximum passband attenuation – ap = 1dB.

Step 2:

Method - filter design using Chebyshev reference analog prototype filter

Step 3:

Filter order is predetermined, N = 3.

Step 4:

The Chebyshev reference prototype filter transfer function has no zeros, only poles. These can be computed via expression:
As N = 3, the values of poles are:
The Chebyshev filter transfer function is expressed as:
In this case, the value of constant A0 is:

A0 = - 0.4913

The reference analog prototype filter transfer function is:
Step 5:

First it is necessary to compute the analog prototype filter cut-off frequency Ωc.
The analog filter transfer function is obtained from the reference analog prototype filter transfer function using expression:
As the Chebyshev reference prototype filter has no zeros, the expression for transfer function is simpler:
After substitution of poles and Ωc into expression:
Step 6:

The transformation into a digital filter through bilinear transformation:
Generally, substituting the complex variable s into the expression for analog filter transfer function, the following is obtained:
where:
zk are the zeros of analog filter transfer function; and
pk are the poles of analog filter transfer function.

This general expression can be written in a simpler way in this example:
A more condensed form of the previous expression is:
The result is the IIR filter transfer function.

Step 7:

The filter order is predetermined.
There is no need to additionally change it.

Filter realization:

Figure 3-6-14 illustrates the direct realization of designed IIR filter.          

3.6.1.3 Example 3

Step 1:

Type of filter – band-pass filter
Filter specifications:
 

• • Filter order – N = 4;

 

• • Sampling frequency – fs = 20KHz;

 

• • Passband cut-off frequencies – fc1 = 4KHz, fc2 = 6KHz; and

 

• • Maximum passband attenuation – ap = 1dB.

Step 2:

Method filter design using Chebyshev reference analog prototype filter.

Step 3:

Filter order is predetermined, N = 4.

Step 4:

The Chebyshev reference prototype filter transfer function has no zeros, only poles. These can be computed via expression:
When designing an IIR band-pass filter, the reference prototype filter order is half that of the required IIR filter order. In this example for N = 4, the order of reference prototype filter is 2, so the values of poles are:
The Chebyshev filter transfer function is expressed as:
In this example, the value of constant A0 is:

A0 = 0.9826

The reference analog prototype filter transfer function is:
Step 5:

First it is necessary to compute the analog prototype filter cut-off frequency Ωc.
The analog filter transfer function is obtained from the reference analog prototype filter transfer function using expression:
As the Chebyshev reference prototype filter has no zeros, the expression for transfer function is simpler:  
Step 6:

The transformation into a digital filter through bilinear transformation:
Generally, substituting the complex variable s into the expression for analog filter transfer function, the following is obtained:
where:
zk are the zeros of analog filter transfer function; and
pk are the poles of analog filter transfer function.

In this expression, the general expression can be written in a simpler way:
A more condensed form of the previous expression is:
The result is the IIR filter transfer function.

Step 7:

Filter order is predetermined.
There is no need to additionally change it.

Filter realization:

Figure 3-6-16 illustrates direct realization of designed IIR filter.          

3.6.1.4 Example 4

Step 1:

Type of filter – band-stop filter
Filter specifications:
 

• • Filter order – N = 4;

 

• • Sampling frequency – fs = 20KHz;

 

• • Passband cut-off frequencies – fc1 = 3000Hz, fc2 = 3300Hz; and

 

• • Maximum passband attenuation – ap = 1dB.

Step 2:

Method - filter design using Chebyshev reference analog prototype filter.

Step 3:

Filter order is predetermined, N = 4.

Step 4:

The Chebyshev reference prototype filter transfer function has no zeros, only poles. These can be computed via expression:
When designing an IIR band-pass filter, the reference prototype filter order is half that of the required IIR filter order. In this example for N = 4, the order of reference prototype filter is 2, so the values of poles are:
The Chebyshev filter transfer function is expressed as:
In this example, the value of constant A0 is:

A0 = 0.9826

The reference analog prototype filter transfer function is:
Step 5:

First it is necessary to compute the analog prototype filter cut-off frequency Ωc.
The analog filter transfer function is obtained from the reference analog prototype filter transfer function using expression:
As the Chebyshev reference prototype filter has no zeros, the expression for transfer function is simpler:  
Step 6:

The transformation into a digital filter through bilinear transformation:
Generally, substituting the complex variable s into the expression for analog filter transfer function, the following is obtained:
where:
zk are the zeros of analog filter transfer function; and
pk are the poles of analog filter transfer function.

In this expression, the general expression can be written in a simpler way:
A more condensed form of the previous expression is:
The result is the IIR filter transfer function.

Step 7:

Filter order is predetermined.
There is no need to additionally change it.

Filter realization

Figure 3-6-18 illustrates the direct realization of designed IIR filter.          

3.6.3 Filter design using inverse Chebyshev filter

 

3.6.3.1 Example 1

Step 1:

Type of filter –low-pass filter
Filter specifications:
 

• • Sampling frequency – fs = 44100Hz;

 

• • Passband cut-off frequency – fc1 = 15KHz;

 

• • Stopband cut-off frequency – fc2 = 18KHz;

 

• • Maximum passband attenuation – ap = 1dB; and

 

• • Minimum stopband attenuation – as = 40dB.

Step 2:

Method - filter design using inverse Chebyshev reference analog prototype filter.

Step 3:

Filter order is not pre-determined, so it is necessary to choose an initial solution from which iterative method starts. The solution is redefined progressively until some pre-determined requirements are satisfied. Let’s assume that the initial filter order is 4.

Step 4:

The Chebyshev reference prototype filter transfer function has no zeros, only poles. These can be computed via expression:
As N = 4, the values of poles are:
The inverse Chebyhsev filter transfer function is expressed as:
In this example, the value of constant H0 is:

H0 = 0.01

so that the Chebyshev reference analog prototype filter transfer function is:
Step 5:

First it is necessary to compute the analog prototype filter cut-off frequency Ωc.
The analog filter transfer function is obtained from the reference analog prototype filter transfer function using expression:
In this example, the analog filter transfer function becomes:  
Step 6:

The transformation into a digital filter through bilinear transformation:
Generally, substituting the complex variable s into the expression for analog filter transfer function, the following is obtained:
where:
zk are the zeros of analog filter transfer function; and
pk are the poles of analog filter transfer function.

This general expression can be written in a simpler way in this example:
A more condensed form of the previous expression is:
The result is the IIR filter transfer function.

Step 7:

By analyzing the resulting filter using Filter Designer Tool, it is obvious that the attenuation amounting to 5.2dB approximately at the frequency of 15KHZ is not sufficient. The frequency characteristic of the resulting digital filter is illustrated in Figure 3-6-20 below.  
The attenuation at 15KHz is higher than 1dB and the resulting filter doesn’t satisfy the specifications therefore. It is necessary to additionally redefine the filter order until the predefined requirements are satisfied. The filter order is incremented by 1, and becomes 5 therefore. All steps starting with step 3 are iterated.

Step 3:

The filter order is incremented in the second iteration. A new filter order is 5.

Step 4:

The inverse Chebyshev reference prototype filter transfer function has no zeros, only poles.

These can be computed via expression:
As N = 5, the values of poles are:
The Chebyhsev filter transfer function is expressed as:
In this case, the value of constant H0 is:

H0 = - 0.05

so the inverse Chebyshev reference analog prototype filter transfer function is:
Step 5:

First it is necessary to compute the analog prototype filter cut-off frequency Ωc.
The analog filter transfer function is obtained from the reference analog prototype filter transfer function using expression:
In this example, the analog filter transfer function becomes:  
Step 6:

The transformation into a digital filter through bilinear transformation:
Generally, substituting the complex variable s into the expression for analog filter transfer function, the following is obtained:
where:
zk are the zeros of analog filter transfer function; and
pk are the poles of analog filter transfer function.

This general expression can be written in a simpler way in this example:
A more condensed form of the previous expression is:
The result is the IIR filter transfer function.

Step 7:

By analysing the resulting filter using Filter Designer Tool, it is obvious that the attenuation at 18KHZ is less than 1dB (approximately 0.8dB). The frequency characteristic of the resulting digital filter is illustrated in Figure 3-6-21 below.  
It is not necessary to further increase the filter order as this one is approriate. Sometimes more iterations are needed to determine the filter order. The whole procedure is the same, only it takes more time.

Filter realization:

Figure 3-6-22 illustrates the direct realization of designed IIR filter, whereas Figure 3-6-23 illustrates the frequency characteristic of the filter obtained using Filter Designer Tool.          

3.6.1.2 Example 2

Step 1:

Type of filter – high-pass filter
Filter specifications:
 

• • Filter order – N = 3;

 

• • Sampling frequency – fs = 20KHz;

 

• • Passband cut-off frequency– fc = 5KHz; and

 

• • Minimum stopband attenuation – 40dB.

Step 2:

Method - filter design using inverse Chebyshev reference analog prototype filter.

Step 3:

Filter order is predetermined, N=3.

Step 4:

The Chebyshev reference prototype filter transfer function has no zeros, only poles. These can be computed via expression:
As N = 3, the values of poles are:
The inverse Chebyshev filter transfer function is expressed as:
In this case, the value of constant H0 is:

H0 = -0.03

The reference analog prototype filter transfer function is:
Step 5:

First it is necessary to compute the analog prototype filter cut-off frequency Ωc.
The analog filter transfer function is obtained from the reference analog prototype filter transfer function using expression:
In this example, the transfer function is:
After substituting the poles and Ωc into expression:
Step 6:

The transformation into a digital filter through bilinear transformation:
Generally, by substituting the complex variable s into the expression for analog filter transfer function, the following is obtained:
where:
zk are the zeros of analog filter transfer function; and
pk are the poles of analog filter transfer function.

This general expression can be written in a simpler way in this example:
A more condensed form of the previous expression is:
The result is the IIR filter transfer function.

Step 7:

The filter order is predetermined.
There is no need to additionally change it.

Filter realization:

Figure 3-6-24 illustrates the direct realization of designed IIR filter.          

3.6.1.3 Example 3

Step 1:

Type of filter – band-pass filter
Filter specification:
 

• • Filter order – N = 4;

 

• • Sampling frequency – fs = 20KHz;

 

• • Passband cut-off frequencies – fc1 = 4KHz, fc2 = 6KHz; and

 

• • Minimum stopband attenuation – 40dB.

Step 2:

Method - filter design using inverse Chebyshev reference analog prototype filter.

Step 3:

Filter order is predetermined, N = 4.

Step 4:

The Chebyshev reference prototype filter transfer function has no zeros, only poles. These can be computed via expression:
When designing an IIR band-pass filter, the reference prototype filter order is half that of the required IIR filter order. In this example for N=4, the order of reference prototype filter is 2, so the values of poles are:
The Chebyshev filter transfer function is expressed as:
In this example, the value of constant H0 is:

H0 = 0.01

The reference analog prototype filter transfer function is:
Step 5:

First it is necessary to compute the analog prototype filter cut-off frequency Ωc.
The analog filter transfer function is obtained from the reference analog prototype filter transfer function using expression:
For this example, the analog filter transfer function is:    
Step 6:

The transformation into a digital filter through bilinear transformation:
Generally, substituting the complex variable s into the expression for analog filter transfer function, the following is obtained:
where:
zk are the zeros of analog filter transfer function; and
pk are the poles of analog filter transfer function.

In this example, the general expression can be written in a simpler way:
A more condensed form of the previous expression is:
The result is the IIR filter transfer function.

Step 7:

Filter order is predetermined.
There is no need to additionally change it.

Filter realization:

Figure 3-6-26 illustrates direct realization of designed IIR filter.          

3.6.1.4 Example 4

Step 1:

Type of filter – band-stop filter
Filter specification:
 

• • Filter order – N=4;

 

• • Sampling frequency – fs=20KHz;

 

• • Stopband cut-off frequencies – fc1=3000Hz, fc2=3300Hz; and

 

• • Minimum stopband attenuation – 40dB.

Step 2:

Method - filter design using inverse Chebyshev reference analog prototype filter.

Step 3:

Filter order is predetermined, N = 4.

Step 4:

The inverse Chebyshev reference prototype filter transfer function has no zeros, only poles. These can be computed via expression:
When designing an IIR band-stop filter, the reference prototype filter order is half that of the required IIR filter order. In this example for N = 4, the order of reference prototype filter is 2, so the values of poles are:
The inverse Chebyshev filter transfer function is expressed as:
In this example, the value of constant H0 is:

H0 = 0.01

The reference analog prototype filter transfer function is:
Step 5:

First it is necessary to compute the analog prototype filter cut-off frequency Ωc.
The analog filter transfer function is obtained from the reference analog prototype filter transfer function using expression:
In this example, the analog filter transfer function is:    
Step 6:

The transformation into a digital filter through bilinear transformation:
Generally, substituting the complex variable s into the expression for analog filter transfer function, the following is obtained:
where:
zk are the zeros of analog filter transfer function; and
pk are the poles of analog filter transfer function.
In this expression, the general expression can be written in a simpler way:
A more condensed form of the previous expression is:
The result is the IIR filter transfer function.

Step 7:

Filter order is predetermined.
There is no need to additionally change it.

Filter realization:

Figure 3-6-28 illustrates the direct realization of designed IIR filter.